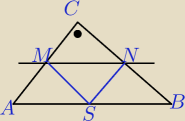
optymalizacyjne, geometria Archeolog: Przeciwprostokątna AB trójkąta prostokątnego ABC ma długość 5, a przyprostokątna BC długość 4. Prosta l, równoległa do boku AB, przecina boki AC i BC odpowiednio w punktach M i N. Niech S oznacza środek odcinka AB oraz |MC| = x. a) Pole P(x) trójkąta MNS jest funkcją zmiennej x. Znajdź wzór tej funkcji. |MC| = x

	5
|AS| = |SB| =
	2

|AC| = 3 , |AB| =5 , |BC| = 4

	5
Obliczyłem też, że |MN| =		*x
	3

Jak teraz zdobyć tą wysokość spadającą z punktu S na bok MN?

Archeolog:

	12−4x
i jeszcze, że |MS| =		.
	3

Archeolog: Mógłbym tak dotrzeć do wzoru Herona, ale te obliczenia prawdopodobnie nie były by za ładne... Nie ma jakiegoś innego sposobu?

Mila: |AB|=5 |BC|=4 |AC|=3 MN=m ΔMNC∼ΔABC

MN		AB		m		5		5x
	=		⇔		=		⇔m=
x		AC		x		3		3

	1
PΔABC=		*3*4=6
	2

	1
PΔABC=		*|AB|*|CD|⇔
	2

	1
6=		*5*|CD|
	2

	12
|CD|=
	5

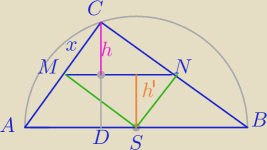
h		|CD|		12
	=		⇔3h=x*
x		3		5

	4x
h=
	5

	12		4
h'=		−		x
	5		5

	1		5x		12		4
PΔMNS=		*		*(		−		x)
	2		3		5		5

	1		x		2
PΔMNS=		*4*		*(3−x)=		*(3x−x2)
	2		3		3

Archeolog: Dzięki wielkie! Zupełnie przegapiłem wysokość ΔMNC.

Mila: Posprawdzaj moje rachunki

Archeolog: Jutro z rana się zajmę tym zadankiem biorąc pod uwagę, że z proporcji mogę wysokość obliczyć