Zapytanie Ala: Uzasadnij, że funkcja f(x)= 2x² + √5x− 1 dla każdego argumentu x∊(1; +∞) przyjmuje wartość większą od 3... Czy mogę napisać, że 2x² + √5x− 1>3 i policzyć miejsca x1 i x2 i pokazać, że są one większe od 1?

Ala: Up

Ala: Up

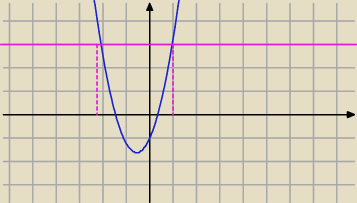
Mila: Parabola skierowana do góry.

	−√5
Wartość najmniejsza dla xw=
	4

	−√5		−√5		−√5
f(		)=2*(		)2+√5*		−1=
	4		4		4

	5		5		5		10		8		13
=2*		−		−1=		−		−		=−
	16		4		8		8		8		8

	−√5
Dla x>		funkcja jest rosnąca
	4

f(1)=2+√5−1= 1+√5>3 zatem dla x>1 funkcja przyjmuje wartości większe od 3. II sposób Parabola skierowana do góry 2x² + √5x− 1=3⇔

	−√5
f(x) rosnąca dla x>
	4

2x²+√5x−4=0

	−√5−√37		−√5+√37
x1=		≈−2,07 lub x2=		≈0.96
	4		4

	−√5−√37		−√5+√37
f(x)>3 dla x<		lub f(x)>3 dla x>		⇔
	4		4

f(x)>3 dla x>1