help! Wydi: Rozpatrujemy wszystkie prostokąty o polu równym 6, których dwa sąsiednie boki zawarte są w osiach Ox i Oy układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą.

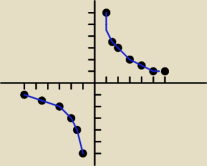
BiebrzaFun : y,x≠0 y*x=6

	6
y=
	x

wykresem będzie część hiperboli dla x∊<−6;6>/{0}

Megi: To nie wszystko

	−6
lub y =		dla punktów: P( −x,y) i P( x, −y)
	x

	−6
gałęzie hiperboli y=		w II ćw. i IV ćw. dla x≠0 i y ≠0
	x

Biebrza skąd to założenie x €<−6,6> ? dla x= 12 y= ¹₂ bo x*y= 6 => 12*¹₂= 6 dla x = 24 y= ¹₄ bo x*y= 6 => 24*¹₄= 6 itd Odp: zbiór takich punktów spełniajacych warunki zadania należy do hiperboli o równaniach:

	6		−6
y =		... lub y =		dla x≠0 i y≠0
	x		x

BiebrzaFun : zgadza się Megi,nie wiem dlaczego tak napisałem

Megi: