#workout 5 PrzyszlyMakler: Zbadaj zbiór wartości funkcji. f(x) = x⁴ − 4x³ +4x² −5

Bogdan: Wyznacz ekstrema funkcji i wyznacz granice funkcji na krańcach dziedziny

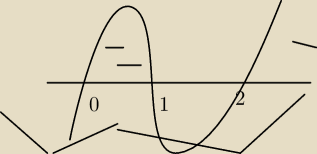
olekturbo: f'(x) = 4x³−12x²+8x = 4x(x²−3x+2) = 4x(x−1)(x−2) f'(x) > 0 ⇔ 4x(x−1)(x−2) > 0 x ∊ (0,1) x ∊ (2,∞) rośnie x ∞ (−∞,0) x ∊ (1,2) maleje dla 0 y_min dla 1 y_max dla 2 y_min f(0) = −5 f(1) = 1−4+4−5 = −4 f(2) = 16−32+16−5 = −5 ZW <−5, −4> jest to dobre rozwiązanie?

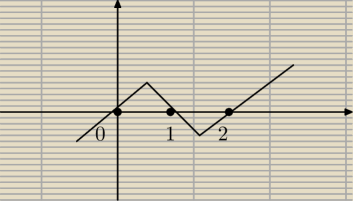
PrzyszlyMakler: f`(x)=4x<sup>3</sup> −12x<sup>2</sup> +8x=0 f`(x)=x(x²−4x+2)=0 x₁ = 2 x₂=1 fmin= f(0)= −5 fmax=f(1)= −4 fmin= f(2) = 16 − 32 + 16 − 5 = −5 f + niesk = fmax Okej, ale dlaczego nie dla f −niesk nie będzie fmin? Tzn, wiem, że jak podstawie np. −100 to nie osiagne mniejszej liczby od −5, ale jak to udowodnić?

Bogdan: Oblicz granice: lim_x→−∞ f(x) i lim_x→+∞ f(x)

PrzyszlyMakler: Granice dla pochodnej czy dla normalnej funkcji?

PrzyszlyMakler: Aaa, normalnej.

PrzyszlyMakler: Ale nie wiem jak to zrobić, gdyż nie idzie pogrupować, ani wyłączyć wspólny czynnik...

olekturbo: x⁴ przed nawias

PrzyszlyMakler: Czaje. Dziękuję.