Wykaż, że
Tom12:
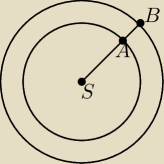
Puknt S jest wspólnym środkiem okręgów o promieniach r = |SA| i R = |SB|, r<R (zobacz
rysunek). Wykaż, że jeśli zwiększymy promień dużego okręgu tak, że długość tego okręgu
wzrośnie o a>0, to długość odcinka AB wzrośnie o wartość, która nie zależy od długości
promieni r i R.
kochanus_niepospolitus:
W sumie ... co tutaj dowodzić trzeba?

wiemy, że:
|AB| = R − r
jeżeli zwiększymy R o jakieś a ... czyli R
nowe = R + a
to
|AB|
nowe = (R+a) − r = R−r + a = |AB| + a
czyli długość odcinka |AB| zwiększyła się o 'a' ... czyli o tyle o ile zwiększono promień
większego okręgu.
Zmiana długości odcinka nie zależy od promieni r i R (a jedynie od 'a' czyli od zmiany
promienia R).
c.n.w.
 Puknt S jest wspólnym środkiem okręgów o promieniach r = |SA| i R = |SB|, r<R (zobacz
rysunek). Wykaż, że jeśli zwiększymy promień dużego okręgu tak, że długość tego okręgu
wzrośnie o a>0, to długość odcinka AB wzrośnie o wartość, która nie zależy od długości
promieni r i R.
Puknt S jest wspólnym środkiem okręgów o promieniach r = |SA| i R = |SB|, r<R (zobacz
rysunek). Wykaż, że jeśli zwiększymy promień dużego okręgu tak, że długość tego okręgu
wzrośnie o a>0, to długość odcinka AB wzrośnie o wartość, która nie zależy od długości
promieni r i R.
 wiemy, że:
|AB| = R − r
jeżeli zwiększymy R o jakieś a ... czyli Rnowe = R + a
to
|AB|nowe = (R+a) − r = R−r + a = |AB| + a
czyli długość odcinka |AB| zwiększyła się o 'a' ... czyli o tyle o ile zwiększono promień
większego okręgu.
Zmiana długości odcinka nie zależy od promieni r i R (a jedynie od 'a' czyli od zmiany
promienia R).
c.n.w.
wiemy, że:
|AB| = R − r
jeżeli zwiększymy R o jakieś a ... czyli Rnowe = R + a
to
|AB|nowe = (R+a) − r = R−r + a = |AB| + a
czyli długość odcinka |AB| zwiększyła się o 'a' ... czyli o tyle o ile zwiększono promień
większego okręgu.
Zmiana długości odcinka nie zależy od promieni r i R (a jedynie od 'a' czyli od zmiany
promienia R).
c.n.w.