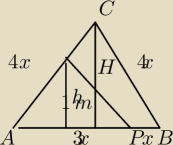
asd olekturbo: Co robię źle? Z punktu P należącego do boku AB trójkąta równobocznego ABC poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta, jaki tworzy ta półprosta z odcinkiem AP, jeśli |AP| : |PB| = 3

	3
Δ1 ~ Δ2 (k=		)
	4

H = 4x√3/2 = 2x√3

	3		3
h =		* 2x√3 =		x√3
	4		2

	h
tga =		= √3
	3   x 2

olekturbo: ref

Metis: A jaka jest odpowiedz?

olekturbo: Nie wiem

olekturbo: Do domu dostałem.

Godzio: Trójkąty nie są podobne, skąd ten wniosek?

olekturbo: Hm. Racja. Sprobuje z pola. Bo pewnie pole małego trójkąta równa się połowie dużego.

Godzio:

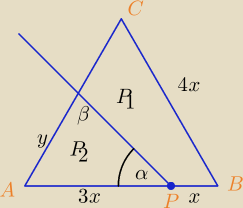
	(4x)2√3
P1 + P2 =		= 4x2√3 oraz P1 = P2
	4

2P₂ = 4x²√3 ⇒ P₂ = 2x²√3

	1
P2 =		* 3x * y * sin60o = 2x2√3
	2

3		√3		8
	xy *		= 2x2√3 ⇒ y =		x
2		2		3

β = 90^o − α Z twierdzenia sinusów:

3x		y		3x		8   x 3
	=		⇒		=
sinβ		sinα		sin(90o − α)		sinα

3		8   3		sinα		8		8
	=		⇒		=		⇒ tgα =
cosα		sinα		cosα		9		9

Eta:

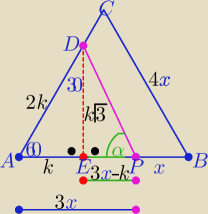
	1
Z treści zadania : P(APD)=		P(ABC)
	2

	1		1		(4x)2√3
to:		* 3x*k√3=		*		⇒ 3√3kx= 4x2√3 /: x>0
	2		2		4

	3
3√3k= 4x√3 ⇒x=		k
	4

	5
|EP|= 3x−k ⇒ |EP|=		k i |ED|= k√3
	4

	k√3		4√3
to tgα=		=
	5   k 4		5

Godzio: Wygląda na to, że sknociłem i nawet widzę co. Nie wiem skąd mi się wzięło, że β = 90^o − α

Godzio: Ety sposób łatwiejszy więc już nie poprawiam, mogę tylko dodać, że u mnie β = 120^o − α, trzeba rozwinąć ze wzoru i sin(120^o − α) i mamy układ równań: twierdzenie sinusów + jedynka trygonometryczna, stąd się wyznaczy to co trzeba.

Metis: A skąd równoległość PD i BC ?

Eta: Metis tam nie ma równoległości !

Metis: No właśnie

Eta: Nawet i na moim rysunku ( jakbyś dobrze popatrzył PD nie jest równoległe do BC

Metis: Wzrok już nie ten sam co kiedyś