 Więc.
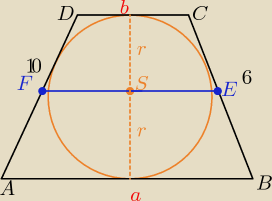
Korzystając z własności czworokąta opisanego na kole:
a + b = 6 + 10
a + b = 16
P = r * [(Obwód)/2]
P = r * 16
Korzystając z wzoru na odległość środkowej trapezu: a + b / 2 = 16 / 2 = 8
Mamy jeden trapez podzielony na dwa mniejsze:
3x/5x = P1/P2
P1 + P2 = 8x
8x = 16r
x = 2r
P1 = 6r
P2 = 10r
P1 (a + 8)r / 2 = 6r
(a + 8)r = 12r
a + 8 = 12
a = 4
b = 16 − 4 = 12
Więc.
Korzystając z własności czworokąta opisanego na kole:
a + b = 6 + 10
a + b = 16
P = r * [(Obwód)/2]
P = r * 16
Korzystając z wzoru na odległość środkowej trapezu: a + b / 2 = 16 / 2 = 8
Mamy jeden trapez podzielony na dwa mniejsze:
3x/5x = P1/P2
P1 + P2 = 8x
8x = 16r
x = 2r
P1 = 6r
P2 = 10r
P1 (a + 8)r / 2 = 6r
(a + 8)r = 12r
a + 8 = 12
a = 4
b = 16 − 4 = 12
| a+b | ||
IEFI= | −− to dł. linii środkowej trapezu
| |
| 2 |
| 16 | ||
a+b = 10+6 = 16 to IEFI= | = 8
| |
| 2 |
| a+8 | 16−b+8 | 24−b | ||||
P1= | *r = | *r= | *r
| |||
| 2 | 2 | 2 |
| 8+b | ||
P2= | *r
| |
| 2 |
| P2 | 3 | |||
= | ||||
| P1 | 5 |
| 8+b | 3 | |||
otrzymamy: | = | |||
| 24−b | 5 |
 Dzięki Wam
Dzięki Wam