geometria analityczna zosia: witam..pomoże ktoś w zadanku? punkt C=(1,−3) jest wierzchołkiem trójkąta równobocznego ABC .Wyznacz współrzędne pozostałych wierzchołków wiedząc,że należą one do prostej o równaniu y=−x+4

kaz: było to zadanie,poszukaj w postach Godzia lub Bogdana

Godzio: https://matematykaszkolna.pl/forum/31272.html tu dokładnie

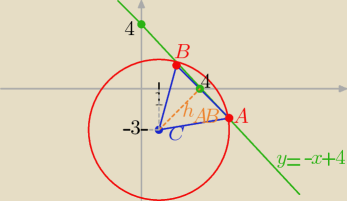
Dag: odległość punktu C od prostej y= −x +4 równa jest długośći h trójkąta równobocznego ABC o boku "a" prosta : −x −y +4=0 C( 1, −3)

	I1*(−1)−3*(−1)+4I		I6I		6*√2
hAB=		=		=		= 3√2
	√1+1		√2		2

	a√3
h=		= 3√2
	2

	6√2
to: a√3= 6√2 => a=		= U{6√6{3}= 2√6
	√3

Rozwiązując układ równań: okręgu C=S( 1, −3) o promieniu r= a z prostą y = −x +4 otrzymamy współrzędne punktów A i B o: ( x −1)² +(y +3)² = 24 i y = −x +4 x² −2x +1 +( 7−x)²= 24 x² −2x +1 +49 −14x +x² −24=0 2x² −16x +26=0 /:2 x² −8x +13=0 Δ= 64 −52= 12 √Δ= 2√3 x₁= 4 +√3 v x₂ = 4 −√3 to y₁= −4 −√3+4 v y₂= −4 +√3+4 y₁= −√3 v y₂= √3 A( 4+√3, −√3) B( 4−√3, √3)

zosia: dziękuje bardzo,