analitycznie
Metis: Zadanka, zadanka...

Cześć

Właśnie przerobiłem geometrie analityczną,
Chcę już sobie to utrwalić

Macie jakieś fajne zadanka do przerobienia?

23 lut 18:16
Meow: jak przejść z równania wektorowego na kierunkowe? Umiesz to wytłumaczyć ?

23 lut 18:20
Metis: Załóż post i powiedz o co Ci dokładnie chodzi

23 lut 18:21
kyrtap: takie coś robiłeś?
Obliczyć pole trójkąta ABC o wierzchołkach A(3,6), B(1,0), wiedząc, że wysokości przecinają się
w punkcie (4,4). Sporządzić rysunek.
23 lut 18:45
Metis: Cześć

Nie, takiego nie

Ale już robię.
23 lut 18:47
Metis: Okey, chyba mam

23 lut 19:07
kyrtap: najgorzej że nie mam odpowiedzi do tego zadania

23 lut 19:09
Metis: Juz wstawiam to zerkniecie

23 lut 19:12
23 lut 19:25
Metis: Sprawdzicie?

23 lut 19:42
kyrtap: sprawdźcie koledze

23 lut 21:55
kyrtap: 
24 lut 16:15
Metis: 
24 lut 16:59
Godzio:
Uno momento
24 lut 17:30
Godzio:
Pomysł dobry, ale coś Ci się pomyliła prosta k i l, oznaczenia powinny być na odwrót.
k − prosta zawierająca AS, a później liczysz prostą prostopadłą do k jako AC, a one nie są
prostopadłe.
24 lut 17:35
Metis: Okey widzę

Reszta

?

24 lut 17:37
olekturbo: Ja mam fajne.

Znajdź zbiór punktów równo oddalonych od okręgu x
2+y
2 = 100 i od punktu A(a,0), gdzie a jest
trzy razy większe od pierwiastków równania:
| | 1 | | 1 | | 3 | |
1 + |
| + |
| + ... = |
| |
| | x−5 | | (x−5)2 | | 4 | |
mi wyszło
(4x−12)
2+25y
2 = 400 ale nie wiem czy mogę zostawić to w takiej postaci
24 lut 17:50
Godzio:
| (x − 3)2 | | y2 | |
| + |
| = 1 −− a to jest elipsa  |
| 25 | | 16 | |
24 lut 17:55
Godzio:
Metis sposób dobry, ale złe wyniki ciągną inne więc właściwie reszta jest cała źle

24 lut 17:56
Metis: Poprawię

dzięki

24 lut 17:59
kyrtap: 
24 lut 18:00
Metis: To równanie utożsamiamy z sumą szeregu geometrycznego.
gdzie a jest trzy razy większe od pierwiastków równania − od sumy? iloczynu?
Co to znaczy

Oczywiście nie wiem czy równanie ma jedno, dwa, czy x rozwiązań.
24 lut 18:02
Metis: Dokładnie to lewą stronę równania.
24 lut 18:04
Godzio:
Równanie ma tylko jeden pierwiastek więc pewnie chodziło trzy raz większy od niego

24 lut 18:04
Metis: zastanawiam się co będzie określało ten nasz zbiór punktów.
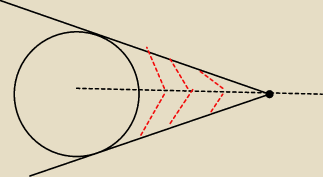
Myślę o stycznych poprowadzonych do okręgu przez punkt A
24 lut 18:15
Metis: Ale to tylko wolne rozważania

24 lut 18:15
olekturbo: Dokładnie
24 lut 18:16
olekturbo: Do Godzia to było

24 lut 18:16
olekturbo: Przyrównaj d1 do d2
24 lut 18:17
Metis:
24 lut 18:17
olekturbo: Ja bym spojrzał na to z tej strony. Mamy okrąg o równaniu x2+y2 = 100.
Środek oznaczmy jako S(0,0). Promień: r = 10. Oprócz tego mamy do dyspozycji punkt, załóżmy
A(6,0).
Punkt oddalony zarówno od okręgu jak i punktu oznaczmy jako P(x,y).
Ile będą wynosiły |PS| i |AS|?
24 lut 18:23
Metis: No skoro
równo oddalony to beda równe

24 lut 18:26
Metis: Nie no pomysł ze styczną do kosza bo to przecież nie beda punkty równoodległe od okregu i
punktu A ...
24 lut 18:28
olekturbo: Wiem, że równe. Ale chodzi o dokładną odległość
24 lut 18:32
Metis: Nie wiem czy chcesz mnie naprowadzić czy po prostu pytasz

PS=[0−x,0−y] = [−x,−y]
AS=[0−6, 0−0] = [−6,0]
|PS|=
√x2+y2
|AS|=6
Chyba dobrze

24 lut 18:41
olekturbo: Zle

i tu i tu
24 lut 18:47
olekturbo: Nie umiem tlumaczyc
24 lut 18:51
Metis: S(0,0)
P(x,y)
A(6,0)
Wektor PS= [0−x, 0−y] ]= [−x, −y]
Wektor AS= [ 0−6, 0−0]= [−6, 0 ]
Długość wektora PS:√(−x)2+(−y)2=√x2+y2
Długość wektora AS: √(−6)2+02=√36=6
?
24 lut 18:53
Mila:
Podam rozwiązanie.
24 lut 22:45
olekturbo: takie cos mam
(4x−12)2+25y2 = 400
ale Godzio podal jak to zamienic
24 lut 22:45
Mila:
| | 1 | | x−5 | | x−5 | |
S=U{ |
| = |
| = |
| |
| | | | x−5−1 | | x−6 | |
4x−20=3x−18
x=2
a=3*2=6
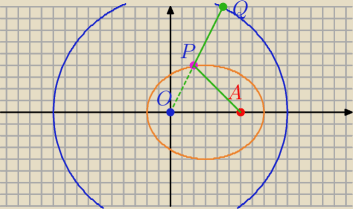
A=(6,0), P(x,y)
|AP|=|PQ|
|AP|=
√(x−6)2+y2
|PQ|=10−|OP|=10−
√x2+y2, |OP|<10 , P∊koła.
√(x−6)2+y2=10 −
√x2+y2 /
2
x
2−12x+36+y
2=100−20
√x2+y2+x
2+y
2
−12x+36=100−20
√x2+y2
−12x−64=−20
√x2+y2/:(−4)
3x+16=5
√x2+y2/
2
9x
2+96x+256=25x
2+25y
2
16x
2−16*6x+25y
2=256 /:16
| (x−3)2 | | y2 | |
| + |
| =1 elipsa |
| 52 | | 42 | |
Takiego zadania, też nie może być na maturze.
24 lut 23:23
Metis: Dziękujemy
Milu 

24 lut 23:26
Mila:
Może być np. takie zadanie:
1)
Znajdź równanie krzywej, którą tworzą wszystkie punkty jednakowo odległe
od okręgu x2+y2−2y=0 i od prostej y+1=0.
2)
Będziecie mieli czas to podam inne.
24 lut 23:30
Metis: Olek nie podawajmy rozwiązania, dopóki nie będziemy mieli go oboje

Ja zajme się nim jutro bo dzisiaj jeszcze muszę napisać rozprawkę

Dziękuje jeszcze raz
Milu 
Jeśli masz jakieś ciekawe zadania, to wstawiaj Nam w ramach przygotowania do matury

Możemy już rozpocząć ten okres na forum.
24 lut 23:35
Mila:

24 lut 23:36
 Cześć
Cześć  Właśnie przerobiłem geometrie analityczną,
Chcę już sobie to utrwalić
Właśnie przerobiłem geometrie analityczną,
Chcę już sobie to utrwalić  Macie jakieś fajne zadanka do przerobienia?
Macie jakieś fajne zadanka do przerobienia? 


 Nie, takiego nie
Nie, takiego nie  Ale już robię.
Ale już robię.







 Reszta
Reszta  ?
? 
 Znajdź zbiór punktów równo oddalonych od okręgu x2+y2 = 100 i od punktu A(a,0), gdzie a jest
trzy razy większe od pierwiastków równania:
Znajdź zbiór punktów równo oddalonych od okręgu x2+y2 = 100 i od punktu A(a,0), gdzie a jest
trzy razy większe od pierwiastków równania:


 dzięki
dzięki 

 Oczywiście nie wiem czy równanie ma jedno, dwa, czy x rozwiązań.
Oczywiście nie wiem czy równanie ma jedno, dwa, czy x rozwiązań.





 PS=[0−x,0−y] = [−x,−y]
AS=[0−6, 0−0] = [−6,0]
|PS|=√x2+y2
|AS|=6
Chyba dobrze
PS=[0−x,0−y] = [−x,−y]
AS=[0−6, 0−0] = [−6,0]
|PS|=√x2+y2
|AS|=6
Chyba dobrze 
 i tu i tu
i tu i tu



 Ja zajme się nim jutro bo dzisiaj jeszcze muszę napisać rozprawkę
Ja zajme się nim jutro bo dzisiaj jeszcze muszę napisać rozprawkę Dziękuje jeszcze raz Milu
Dziękuje jeszcze raz Milu  Jeśli masz jakieś ciekawe zadania, to wstawiaj Nam w ramach przygotowania do matury
Jeśli masz jakieś ciekawe zadania, to wstawiaj Nam w ramach przygotowania do matury  Możemy już rozpocząć ten okres na forum.
Możemy już rozpocząć ten okres na forum.
