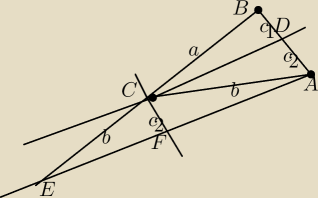
udowodnij koteł: Dany jest trójkąt ABC. długość boku BC to a, długość boku AC to b. Prosta C₁ jest przedłużeniem dwusiecznej kąta ACB. Przecina ona bok AB w punkcie D, dzielą go na odcinek o długości c₁ i c₂. Prosta równoległa do dwusiecznej CD przechodząca przez punkt A przecina prostą CB w punkcie E. Prosta równoległa do AB i przechodząca przez C przecina prostą AE w punkcie F. a) udowodnij ze trójkąt EFC jest podobny do trójkąta CDB. b) udowodnij ze |CE|=b c) udowodnij ze |CF|=c₂ d) Korzystając z podobieństwa trójkątów EFC I CDB pokaż ze a/b = c₁/c₂

koteł: Prosze o pomoc.

Kotel: Pomozcie.

kochanus_niepospolitus: (a) udowodnienie tego jest prozaicznie proste, wystarczy pokazać, że: ∡FEC = ∡DCB (a jako że |AE| || |CD| to mamy już to udowodnione − wystarczy napisać na jakie tw. się powołujemy) oraz :∡FCE = ∡DBC (analogicznie) wtedy trzeci kąt także jest taki sam ... i mamy podobieństwo KKK

kochanus_niepospolitus: (b) należy wykazać, że ∡ACD = ∡DAC = α (z jakiego tw. korzystamy) Skoro C₁ jest dwusieczną ∡ACB, to ∡ACD = ∡DCB Natomiast w (a) wykazaliśmy, że ∡FEC = ∡DCB A więc otrzymujemy: ∡AEC = ∡EAC = α ... czyli Δ_AEC jest równoramienny ... skoro |AC| = b to i |CE| = b

kochanus_niepospolitus: (c) |CF| || |AD| , stąd wynika (po zastosowaniu trygonometrii), że |CD| = |EF| Powtórnie korzystając z trygonometrii wyznaczamy |CF| = |AD|

kochanus_niepospolitus: (d) piszesz ... korzystając z podobieństwa trójkątów i piszesz to do końca nie wiem co tutaj niby więcej trzeba zrobić