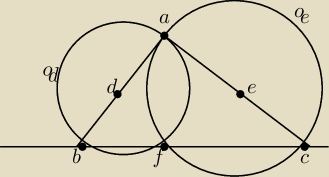
udowodnij koteł: Dany jest trójkąt ABC. Niech środkiem odcinka AB będzie punkt D, a środkiem boku AC − punkt E. Bok AB jest średnica okręgu o_D o środku w D i promieniu AD, a bok AC jest średnicą okręgu o_E o środku w E i promieniu AE. zobacz rysunek. Okręgi o_D i o_E przecinają się w dwóch punktach. Jednym z tych punktów jest A. Udowodnij ze drugi punkt przeciecia tych okręgów leży na prostej BC i jest spodkiem wysokosci trójkąta ABC opuszczonej z punktu A

irena_1: Kąt AFB ora kąt AFC to kąty w tych okręgach oparte na średnicach, więc kąty proste Kąt AFC to suma kątów AFB i AFC. Jest to kąt półpełny. Stąd− punkty B, F i C są współliniowe, czyli F leży na boku BC. Kąt AFB jest prosty, więc AF jest prostopadły do BC− jest wysokością trójkąta, czyli F jest spodkiem wysokości opuszczonej z punktu A.