Udowodnij
koteł:
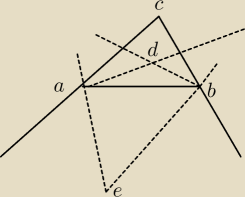
na rysunku przedstawiony jest trojkąt ABC. punkt D jest przecięciem dwusiecznej kąta
wewnętrznego przy wierzchołku A i dwusiecznej kąta wewnętrznego przy wierzchołku B. Punkt E
jest punktem przecięcia dwusiecznych dwóch zewnętrznych kątów trójkąta − przy wiekrzchołku A i
przy wierzchołku B.
a) udowodnij ze punkt E leży na dwusiecznej wewnętrznego kąta trójkąta przy wierzchołku C.
b) udowodnij ze kąty między dwusieczną kąta wewnętrznego dwusieczną kąta zewnętrznego przy
jednym wierzchołku są proste, czyli że na rysunku kąty DAE i EBD są proste.
c) Pokaż że kąty AEB+ADB=180 (stopni)
d) udowodnij ze kąty EAB+ABE = AD