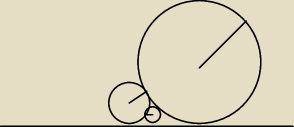
 Trzy okręgi są styczne do jednej prostej, a jednoczesnie sa syyczne do siebie. Przedstawione na
rysunku.
Jeśli znamy promień R i r, to trzeci promień δ mozna wyliczyć z wzoru: U{1}√δ = U{1}√R =
U{1}√r
a) udowodnij wzór
Trzy okręgi są styczne do jednej prostej, a jednoczesnie sa syyczne do siebie. Przedstawione na
rysunku.
Jeśli znamy promień R i r, to trzeci promień δ mozna wyliczyć z wzoru: U{1}√δ = U{1}√R =
U{1}√r
a) udowodnij wzór
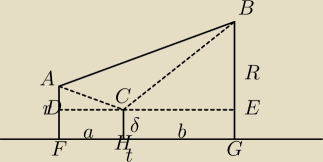 nie rysowałam okręgów, tylko ich środki : A, B, C
|AB|=R+r
|AC|=r+δ
|BC|=R+δ
|AD|=r−δ
|BE|=R−δ
|DE|=t
t2=(R+r)2−(R−r)2=4Rr
t=2√Rr
a2=(r+δ)2−(r−δ)2=4rδ
a=2√rδ
b2=(R+δ)2−(R−δ)2=4Rδ
b=2p{Rδ)
t=a+b
2√Rr=2√Rδ+2√rδ
√R*√r=√R*√δ+√r*√δ
nie rysowałam okręgów, tylko ich środki : A, B, C
|AB|=R+r
|AC|=r+δ
|BC|=R+δ
|AD|=r−δ
|BE|=R−δ
|DE|=t
t2=(R+r)2−(R−r)2=4Rr
t=2√Rr
a2=(r+δ)2−(r−δ)2=4rδ
a=2√rδ
b2=(R+δ)2−(R−δ)2=4Rδ
b=2p{Rδ)
t=a+b
2√Rr=2√Rδ+2√rδ
√R*√r=√R*√δ+√r*√δ
| √R*√r | |
=√R+√r | |
| √δ |
| 1 | 1 | 1 | |||
= | + | ||||
| √δ | √r | √R |