pole największe prostokąta 1moment: Dany jest trójkąt ABC, w którym kąt ACB ma 90 stopni. Boki mają długości: a = 3, b = 4, c = 5. Na przeciwprostokątnej obrano punkt F. W trójkąt wpisano prostokąt tak, że wierzchołkami są punkty C oraz F. Dwa boki tego trójkąta leżą na przyprostokątnych trójkąta. Wyznacz wymiary prostokąta takie, aby miał pole największe.

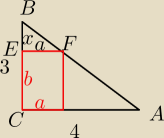
irena_1: x=3−b Trójkąt EFB jest podobny do trójkąta ABC

3−b		3
	=
a		4

12−4b=3a 4b=12−3a

	3
b=3−		a
	4

0<a<4 P=ab

	3		3
P(a)=a(3−		a)=−		a2+3a
	4		4

Funkcja P(a) to funkcja kwadratowa, której wykresem jest część paraboli o ramionach skierowanych w dół. Taka funkcja przyjmuje największą wartość w wierachołku tej paraboli

	−3
aw=		=2
	−2*34

a=2

	3		3
b=3−		=		=1,5
	2		2

a=2 i b=1,5

1moment: Dziękuję serdecznie

irena_1:

1moment: Proszę Pani, mam jeszcze pytanie. Dlaczego w przedostatniej linijce b = 3 − 3/2. Skąd wzięło się to 3/2? Dlaczego tak?

1moment: i jakie znaczenie ma zapis 0< a <4 ? Czy jest on konieczny?