nierówność z wart. bezwzględną
Tomek: Cześć, mam kłopot z rozwiązaniem tego zadania.
Znajdź zbiór rozwiązań nierówności x
3 + 3|x| + x ≥0 Dla mnie wychodzi że x∊<0;
∞) a w
odpowiedziach jest, że x∊<−
√2;
∞). Prosze was o pomoc

22 lut 22:54
Qulka:
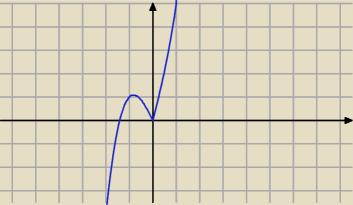
22 lut 22:59
yyhy: 1. x≥0
wtedy x2+3+1≥0 ok
2. x<0 to
x3−3x+x=x3−2x=x(x2−2)=x(x−√2)(x+√2)≥0 gdy x∊[−√2,0)
Łącznie to co ma być
22 lut 23:00
Tomek: ja zrobiłem to tak:
dla x ≥0 doszedłem do takiej nierówności x(x
2+4) ≥ 0 czyli x∊<0;
∞)
dla x < 0 x(x
2 − 2 ) ≥ 0 x ∊ <−
√2;0> U (
√2;
∞) i jak łącze te dwa przedziały to wychodzi
x∊<0;
∞), nie bardzo rozumiem gdzie robie błąd

22 lut 23:06
Qulka: sumujesz te dwa przedziały więc z drugiego masz od −√2 do 0 a z pierwszego od 0 do∞ więc w
sumie jak w odp
22 lut 23:09
Tomek: Bo coś mi się poknociło, że przedział z x≥0 wyłączy już ten <−√2;0>
22 lut 23:12


