Proszę o pomoc
hani: W czworokącie ABCD dane są: |AB|=3, |BC|=4, |CD|=12, |DA|=13 i |AC|=5.
Oblicz cosinus kąta DAB i długość drugiej przekątnej.
Doszłam do tego, że trójkąty ABC i ACD są prostokątne ( twierdzenia pitagorasa),
ale nie wiem co dalej zrobić. Proszę o pomoc.
22 lut 20:49
hani: up
22 lut 21:05
Eta:
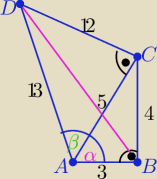
| | 4 | | 12 | | 3 | | 5 | |
sinα= |
| , sinβ= |
| , cosα= |
| , cosβ= |
| |
| | 5 | | 13 | | 5 | | 13 | |
cos(DAB)=cos(α+β)= cosα*cosβ−sinα*sinβ =...............
z twierdzenia cosinusów w trójkącie ABD:
|BD|
2= 13
2+3
2−2*13*3*cos(α+β)=....................
22 lut 21:25
hani: Dziękuję bardzo
Mam jeszcze jedno zadanie, które nie wiem jak zrobić:
Boki trójkąta mają długości 5, 6 i 7. Oblicz:
a) długość środkowej poprowadzonej do boku o długości 6,
b) promień okręgu opisanego na tym trójkącie i promień okręgu wpisanego w ten trójkąt
22 lut 21:45
Eta:
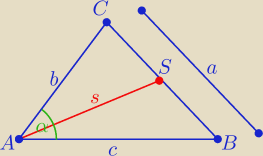
Ze wzoru na długość środkowej ( możesz go wyprowadzić z tw. kosinusów
| | 1 | |
|AS|=s= |
| √2c2+2b2−a2=....................... |
| | 2 | |
| | c2+b2−a2 | |
cosα= |
| = .... to sinα= +√1−cos2α=... |
| | 2bc | |
| | a | |
z tw. sinusów : 2R= |
| =.... |
| | sinα | |
| | 2P | | 1 | |
rw= |
| , P= |
| c*b*sinα =..... |
| | a+b+c | | 2 | |
r
w=....
teraz tylko ......dokończ obliczenia .........
22 lut 22:02
22 lut 22:04
hani: jeszcze raz dziękuję : )
22 lut 22:21
Eta:
Na zdrowie ...
22 lut 22:22
Kacper:
23 lut 07:19