plani
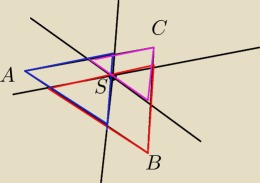
olekturbo: Dany jest trójkąt ABC i punkt S leżący wewnątrz tego trójkąta. Przez punkt S poprowadzono
proste równoległe do boków trojkąta. Otrzymano trzy trójkąty o polach 9, 16 i 25. Oblicz pole
trójkąta ABC.
22 lut 20:24
Metis:
22 lut 20:41
Metis: Fajne zadanko
No i pewnie bez podobieństwa go nie ruszymy.
22 lut 20:41
===:
a rozumiesz skale prawdopodobieństwa
22 lut 20:42
Janek191:
Co to jest ?
22 lut 20:43
olekturbo: Nie rozumiem
22 lut 20:49
Metis: Chyba skala podobieństwa
22 lut 20:50
olekturbo: A mógłby ktoś szerzej omówić ten przypadek ?
22 lut 20:55
olekturbo: ref
22 lut 21:22
Eta:
P(ABC)= P
P=(√S1+√S2+√S3)2
P= 144 [j2]
22 lut 21:46
olekturbo: Dlaczego tak
22 lut 22:26
olekturbo: Eta
22 lut 23:03
Eta:
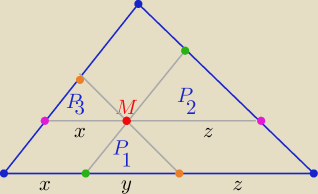
| | y | |
Trójkąt o polu P1 podobny do trójkąta ABC w skali k1= |
| |
| | x+y+z | |
| | z | |
trójkąt o polu P2 podobny do trójkąta ABC w skali k2= |
| |
| | x+y+z | |
| | x | |
trójkąt o polu S3 podobny ...... w skali k3= |
| |
| | x+y+z | |
| | x+y+z | |
k1+k2+k3= |
| =1 ⇒ √S1+√S2+√S3= √P |
| | x+y+z | |
to
P= (√S1+√S2+√S3)2
w tym zadaniu :
P=(3+4+5)
2= 144
22 lut 23:13
olekturbo: dziekuje bardzo
22 lut 23:15
Eta:
Przepraszam
Na rys. miały być oznaczenia S
1, S
2, S
3 −−−pola danych trójkątów
22 lut 23:16
olekturbo: Nie miałem pomysłu na to zadanie
22 lut 23:18
Eta:
A teraz ? ........
22 lut 23:20
olekturbo: Teraz juz wszystko jasne
Dziekuje
Planimetria dla mnie najgorszy dział z matematyki
22 lut 23:21
Metis: Dokładnie
Na drugim probabilistyka
22 lut 23:22
olekturbo: Kombinatoryka jeszcze kuleje.
22 lut 23:24
olekturbo: I fizyka
22 lut 23:24
Eta:
planimetria −−−− prawdziwa matematyka!
Najbardziej dla mnie lubiana
22 lut 23:24
olekturbo: trochę racji w tym jest. Równania, nierówności i tym podobne to głównie jakiś schemat i zależy
od praktyki a w stereometrii czy planimetrii oprócz doświadczenia jeszcze ogromny spryt.
Tego trochę brakuje i może jeszcze z teorią słabo
22 lut 23:27
Kacper:
23 lut 07:13
Eta:
23 lut 16:45