pole największe prostokąta
James Morgan: Dany jest trójkąt ABC, w którym kąt ACB = 90 stopni. Boki mają długości: a = 3, b = 4, a c = 5.
Na przeciwprostokątnej obrano punkt F. W trójkąt wpisano prostokąt tak, że wierzchołkami są
punkty F i C. Dwa boki tego trójkąta leżą na przyprostokątnych.
Wyznacz wymiary prostokąta o polu najwiekszym.
22 lut 19:31
===:
przepisać porządnie treść zadania to duuuuuuuuża sztuka

22 lut 19:42
James Morgan: Naprawdę nie wiem, jak się za to zabrać

22 lut 19:43
James Morgan: oznaczyć boki prostokąta jako 4−x i 3−y... może od tego zacząć?

22 lut 19:45
James Morgan: wówczas jego pole to 12xy
22 lut 19:46
James Morgan: Ale co dalej?

22 lut 19:46
===:
spróbuj narysować to co napisałeś
22 lut 19:49
===:
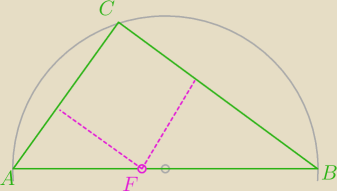
22 lut 19:56
James Morgan:
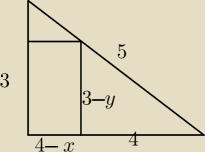
i
22 lut 19:59
===:
powstałe trójkąty są podobne ...baw się skalą podobieństwa
22 lut 20:00
===:
| | 4 | |
jeśli AF oznaczymy jako x to jeden z boków prostokąta jest |
| x |
| | 5 | |
| | 3 | |
|BF|=5−x to drugi z boków prostokąta jest równy |
| (5−x) |
| | 5 | |
22 lut 20:05
===:
| | 12 | | 12 | | 12 | |
S= |
| x(5−x)=− |
| x2+ |
| x |
| | 25 | | 25 | | 5 | |
| | −12 | | −25 | | 5 | |
Smax dla xw= |
| * |
| = |
| |
| | 5 | | 24 | | 2 | |
22 lut 20:11
James Morgan: 12 − y(3−x) = [(3−x)(y + xy)/2
.
.
.
−y2 + 4y − 16 = 0
f'(y) = −2y + 4
y = 2
22 lut 20:15
James Morgan: i teraz x = 3/4 * 2 = 1,5
zatem Pprostokata = x*y = 1,5 * 2 = 3

22 lut 20:16
James Morgan: * 12 − y(3−x) = [(3−x)(y + xy)]/2
22 lut 20:18
===:
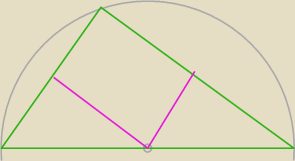
22 lut 20:22





 i
i

