|x +a| = 1 − ||x−2|−3|
NICK99: Dla jakich wartości parametru a równanie |x +a| = 1 − ||x−2|−3| ma dokładnie dwa rozwiązania?
Czy mogę to rozkładać w ten sposób? :
|x +a| = 1 − |x−2|−3 lub |x +a| = 1 − |x−2|+3
|x +a| = −|x−2|+4 lub |x +a| = −|x−2| −2
22 lut 15:37
yyhy: Zacznij od rysunku
y=1−||x−2|−3|
22 lut 15:49
===:
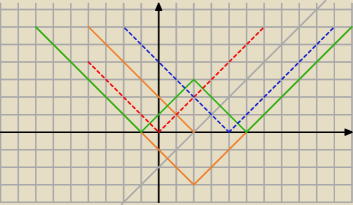
22 lut 15:54
NICK99: Czy ten wykres jest dobry? Bo mi wychodzi trochę inaczej − jak jest odbicie − ||x−2|−3| (ten
minus to symetria względem osi OY ? ) i potem to przesunięcie o 1 w lewo ?
23 lut 11:48
prosta:
przesunięcie o 1 w górę
23 lut 11:53
prosta:
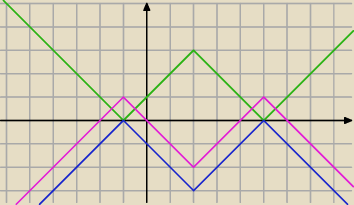
fioletowy wykres jest właściwym wykresem
23 lut 11:58
NICK99: Czyli odbicie od osi OX , ok
Dziękuje za pomoc!
23 lut 12:03