Krótkie zadanko z wielomianów
Karolina: Liczby całkowite a, b, c, d będące pierwiastkami wielomianu W(x) = x4−10x2+p tworzą ciąg
arytmetyczny. Wyznacz te liczby i wartość parametru p.
Próbowałam zapisać b jako a+ r, c jako a+ 2r i potem tworzyć układ równań, ale to chyba jest
błędne bo w zadaniu nie jest napisane ze to są kolejne wyrazy ciągu?
21 lut 11:37
jajcarz: Przecież jest napisane, że są kolejnymi wyrazami ciągu

21 lut 11:52
Bogdan:
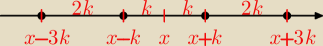
W(x) = (x + 3k)(x + k)(x − k)(x − 3k) = (x
2 − 9k
2)(x
2 − k
2) = x
4 − 10k
2x
2 + 9k
4
−10k
2 = −10 ⇒ k
2 = 1 ⇒ k = −1 lub k = 1
p = 9k
2 = 9
a
1 = −3k = 3 lub a
1 = −3
a
2 = −k = 1 lub a
2 = −1
a
3 = k = −1 lub a
3 = 1
a
4 = 3k = −3 lub a
4 = 3
21 lut 11:56
Kacper:
Brakuje takiego sformułowania, ale potraktuj, że a, b, c, d,
w podanej kolejności są
kolejnymi wyrazami ciągu arytmetycznego.

21 lut 11:57
Karolina: Nie rozumiem za bardzo tego rozwiązania z "k"

dlaczego pierwiastki tego równania to −3k,−k,k
i 3k?
21 lut 12:42
===:
Zauważ, że licząc pierwiastki W(x) możesz zastosować podstawienie
x2=t gdzie t>0
Aby W(x) miało 4 pierwiastki t2−10t+p=0 musi mieć dwa pierwiastki i oba dodatnie
... oczywistym więc jest, że W(x) musi wtedy być f. parzystą a pierwiastki symetryczne
do osi 0y ... dodatkowo mają one tworzyć ciąg arytmetyczny
21 lut 12:58

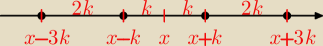 W(x) = (x + 3k)(x + k)(x − k)(x − 3k) = (x2 − 9k2)(x2 − k2) = x4 − 10k2x2 + 9k4
−10k2 = −10 ⇒ k2 = 1 ⇒ k = −1 lub k = 1
p = 9k2 = 9
a1 = −3k = 3 lub a1 = −3
a2 = −k = 1 lub a2 = −1
a3 = k = −1 lub a3 = 1
a4 = 3k = −3 lub a4 = 3
W(x) = (x + 3k)(x + k)(x − k)(x − 3k) = (x2 − 9k2)(x2 − k2) = x4 − 10k2x2 + 9k4
−10k2 = −10 ⇒ k2 = 1 ⇒ k = −1 lub k = 1
p = 9k2 = 9
a1 = −3k = 3 lub a1 = −3
a2 = −k = 1 lub a2 = −1
a3 = k = −1 lub a3 = 1
a4 = 3k = −3 lub a4 = 3

 dlaczego pierwiastki tego równania to −3k,−k,k
i 3k?
dlaczego pierwiastki tego równania to −3k,−k,k
i 3k?