Napisz rownanie stycznych do wykresów podanych funkcji we wskazanych punktach Misiek13141: Napisz rownanie stycznych do wykresów podanych funkcji we wskazanych punktach ktoś mogłby mi wytłumaczyć\ f(x)=1/x, (1,f(1)) f(x)=ln(x2+e) , (0,f(0))

===:

	1
f(x)=
	x

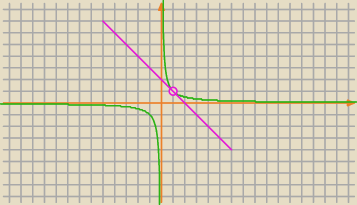
f(1)=1 zatem punkt styczności to S=(1, 1)

	1
f'(x)=−
	x2

f'(1)=−1 szukana styczna ma zatem współczynnik kierunkowy a=−1 i przechodzi przez punkt S=(1, 1) czyli y−1=−1(x−1) ⇒ y=−x+2

Misiek13141: dzieki

===: z drugim poradzisz sobie?

Misiek13141: Jeśli mozesz to wolał bym żebyś rozpisał/a to bym był pewien czy dobrze to robie

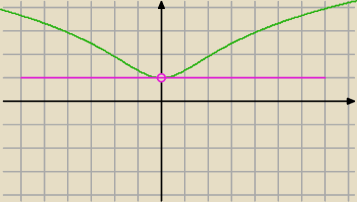
===: f(x)=ln(x²+e) f(0)=lne=1

	2x
f'(x)=
	x2+e

f'(0)=0 Twoja styczna ma zatem współczynnik równy 0 (stała) i przechodzi przez (0, 1) y=1

5-latek: No i co Misiek upewniles się ze masz dobrze ?

Misiekq: A czemu tam jest 2x

===: bo Twoja funkcja to f(x)=ln(x²+e) a nie ln(x)

Misiekq: Ok dzięki