pochodne i styczne Archeolog: Znaleźć równanie prostej stycznej do wykresów funkcji f(x) = x²+1 i g(x) = (x−1)²−1. Próbowałem policzyć pochodne tych dwóch funkcji i przyrównać, ale wychodzi mi 0 = −2.

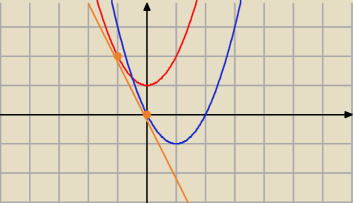
kochanus_niepospolitus: Jeżeli masz problem to na początek narysuj sobie te dwie parabole Zauważysz, że jedyna szansa dla której jedna prosta będzie styczna do obu parabol jest wtedy gdy będzie ona malejąca (czyli f'(x₀) = g'(x₁) <0) teraz postaraj się jeszcze chwilę pokombinować, jak nie dasz rady, to dodam dalsze 'naprowadzenie'.

Archeolog: Aha czyli f'(x1) = g'(x2)... x1 = x2−1 i teraz rozumiem drugie równianie z b i powinno wyjść z tego układu? Z obrazka widać że b =0, ale założę że tego nie wiem i wyznaczę obydwa b dla x2 i x1.

kochanus_niepospolitus: dokładnie ... załóż że tego nie wiesz

Archeolog: Dostajemy 2 punkty, A = (−1,2) i B = (0,0). Czyli prosta y = −2x to nasza szukana styczna do tych wykresów funkcji. Super ten dział jest

kochanus_niepospolitus: No widzisz ... na przyszłość: Nim zaczniesz rozwiązywać −−− robisz szkic wykresu gdybyś zrobił (chociażby) szkic ... to byś wiedział że styczna nie będzie w tym samym punkcie (czyli x₁ = x₂) Zauważ, że (nieświadomie) potraktowałeś, że funkcja f(x) i g(x) mają jednakową styczną w tym samym punkcie 'x' co przy parabolach jest możliwe tylko i wyłącznie jeżeli mają te same współrzędne wierzchołka paraboli.

Archeolog: ja ogółem zrobiłem taką głupotę, że miałem te 2x1 = 2x2−2 i w następnej linijce zapisałem jako 2x = 2x−2 i z tego się ta cała tragedia stała... I jeszcze jeden błąd jak próbowałem inaczej liczyć to zapisałem −x1²+1 = −x2² i dla wygody po pomnożeniu przez −1 zapisałem tamto jako x1²+1 = x2² i znów coś mi nie pasowało...

Jerzy: Rozwiązanie ..." z przymrużeniem oka"