zadanie optymalizacyjhne biale_buty: Znaleźć wymiary prostopadłościanu o sumie krawędzi równej 48, którego objętość jest największa. Wiem, że trzeba użyć ekstremów funkcji wielu zmiennych, ale nie wiem w jaki sposób dokładnie. Czy warunkowe, czy na obszarze? Nigdy wcześniej takiego zadania nie robiłem, a niestety trafiło się na egzaminie, egzaminu już nie poprawię, ale chciałbym przynajmniej wiedzieć jak to należało rozwiązać.

kochanus_niepospolitus: o sumie krawędzi równej 48? a może chodzi o sumę DŁUGOŚCI krawędzi równej 48?

biale_buty: Tak, oczywiście

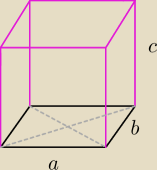
Jack: 4a + 4b + 4c = 48 a + b + c = 12 −>>> a = 12 − b − c V = a * b * c = (12−b−c)bc = 12bc − b²c −c²b V = − b²c − c²b + 12bc jesli nie wiemy nic (aczkolwiek obstawiam ze to szescian bedzie) no to pochodna po b,po c, uklad rownan...

biale_buty: żadnych warunków nie trzeba tworzyć, że np, a,b > x ,żeby to zadanie miało sens? Też obstawiałem, że to sześcian, ale nie potrafiłem obliczyć.

Jack: x? zalezy co to iks... jedyne warunki to a,b,c > 0 12 − b − c> 0 b+c<12 to pochodne jedziem...

dV
	= −2bc − c2 + 12c
db

dV
	= −b2 − 2bc + 12b
dc

{−2bc − c² + 12c = 0 {−b² − 2bc + 12b = 0

Jack: wszystkie odp z zerami odrzucamy, bo b i c> 0 wiec zostaje tylko b = 4, c = 4 czyli nasz punkt P (4,4) (tam jest prawdopodobnie ekstremum) miales wyznacznik macierzy itd?

biale_buty: Tak, tak − miałem, na egzaminie próbowałem to robić ekstremum warunkowym (nie pamiętam jaki warunek wymyśliłem) i mnożnikami Lagrangea, a potem hesjan obrzeżony, ale nic nie wyszło. Dzięki za rozwiązanie, zaraz jeszcze sam to spróbuję zrobić.