Jaką figurą będzie obraz kwadratu w powinowactwem prostokątnym? Adam: Mam prośbę o pomoc przy podpunkcie c) zad. 4.93 ze str. 119 z rozszerzonego zbioru zadań do klasy pierwszej Oficyny Edukacyjnej * Krzysztof Pazdro. Treść zadania jest taka: Jaka figura jest obrazem kwadratu K w pewnym powinowactwem prostokątnym o skali k, k≠0 i |k|≠1, jeśli oś tego powinowactwa nie jest równoległa do żadnego boku kwadratu ani do żadnej przekątnej? Jest to równoległobok, tylko jak to udowodnić, ze to równoległobok?

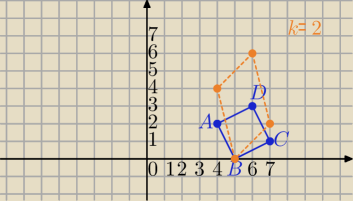
iryt: Powinowactwo o osi OX i skali k, gdzie |k|≠1 i k≠0 Obrazem dowolnego punktu płaszczyzny P(x,y) jest punkt P(x',y') gdzie x'=x

	1
y'=k*y stąd x=x' i y=		y'
	k

Obrazem prostej w powinowactwie jest prosta. AB⊥AD AB: y=ax+b₁, a≠0

	1
AD: y=−		x+b2
	a

Obrazy prostych :

	1
A'B' :		y'=ax'+b1 /*k⇔
	k

y'=a*kx'+k*b₁

	1		1
A'D' :		y'=−		x'+b2 /*k
	k		a

	k
y'=−		x'+k*b2
	a

Iloczyn wsp. kierunkowych:

	k
a*k*−		=−k2 i k2 ≠1 zatem proste A'B' i A'D' nie są prostopadłe.
	a

2) własność : ( możesz to łatwo wykazać.) Obrazem prostych równoległych są proste równoległe , zatem obrazem kwadratu jest równoległobok. AB||DC to A'B'||D'C" AD||BC to A'D'||B'C' 2) powinowactwo P_OY^k x'=kx y'=y Analogiczny dowód.