Trójkąt Ooo: Rozpatrujemy wszystkie trójkąty równoramienne ostrokatne wpisane w okrąg o promieniu długości 2. Wyznacz długość wysokości tego z rozpatrywanych trójkątów, którego pole jest największe , oraz oblicz to pole.

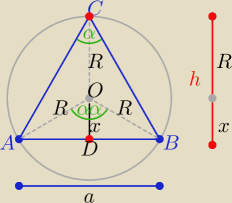
Eta: R=2

	a
Z tw. sinusów w Δ ABC		=2R ⇒ a=2R*sinα ⇒ a=4sinα
	sinα

	x
oraz w ΔADO		= cosα ⇒ x= 2cosα
	R

h=R+x ⇒ h= 2(1+cosα)

	a*h
P(ABC)=		⇒ P(α)=4sinα(1+cosα)
	2

i α∊(0^o,90^o) bo Δ ostrokątny z treści zadania P^'(α)= 4cosα(1+cosα)+ 4sinα*(−sinα) = 4cosα+4cos²α−4sin²α P^'(α)=0 ⇒ ................... ................................ dokończ odp: α= 60^o więc trójkąt ABC jest równobocznym h= 2(1+cos60^o)=............... = 3