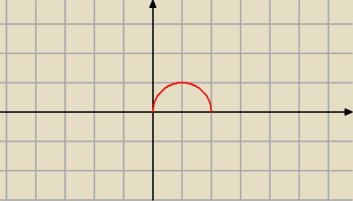
Wyznacz ekstrema lokalne funkcji jag0da: y= √2x−x²

Jerzy: 1) dziedzina 2) pochodna

jag0da: Znam zasadę liczenia, ale zatrzymuje się na wyliczeniu pochodnej i nie wiem co na wyjść z przyrównania do zera.

Janek191: Otrzymasz punkt, w którym funkcja może mieć ekstremum.

Janek191:

	2 − 2 x		1 − x
f '(x) =		=		= 0 ⇔ x = 1
	2√ 2 x − x2		√2 x − x2

Janek191: Mianownik jest > 0 , więc znak pochodnej zależy od licznika: Dla x < 1 jest f '(x) > 0 − f rośnie Dla x > 1 jest f '(x) < 0 − f maleje Dlatego w punkcie x = 1 funkcja f ma maksimum równe f(1) = 1.

Janek191: ?