kwadratowa z parametrem Godzio: Wyznacz te wartości parametru m (m∊R) dla których jeden z pierwiastków równania mx² − (2m+1)x + m −2=0 jest ujemny a drugi większy od 5 czy taki zapis jest poprawny ? x₁<0 x₂ > 5 x₁*x₂ < −5

Godzio: mam nadzieję że ktoś tam jeszcze został

Li : Pomagam

Li : Pomagam z przyjemnością dla Ciebie Godzio Taki zapis jest błędny: 1/ m≠0 2/ Δ>0

	c
3/ x1*x2 <0 =>		<0
	a

z tych trzech warunków otrzymasz m€(0,2) dochodzi 4/warunek wiemy już ,że parabola ramionami zwrócona do góry aby miejsce zerowe x₂ było >5 to f( 5) <0 9 wtedy będzie poza piątką na prawo f( 5)= ...... dokończ odp: m€ (0, ⁷₁₆)

Li : Chochlik wpisał f(5) <0 ..... 9 zamiast (

Godzio: ok dzieki wielkie

Paweł: Li wytłumacz dokładnie jak będzie z tym, że miejsca zerowe będe większe od 5 bo ciekawy przykład.

Eta: Godzio czy zrozumiałeś to zadanie ?

Godzio: raczej tak

Paweł: To wytłumaczycie jak to jest?

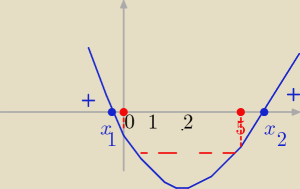
Eta: Do Pawła: z pierwszych trzech warunków mamy: m € (0,2) −−− to parabola ramionami zwrócona do góry więc: x₂ >5 <=> f(5) <0 i x₁ <0 <=> f( 0) <0

Godzio: ja mam jeszcze pytanie, czy na maturze jeśli narysuje wykres, wszystko jest ok tylko nie zaznacze strzałek i osi to czy za to będą obniżane punkty?

R.W.16l: Raczej tak

Paweł: Eta dzięki A powiedz mi jeszcze dlaczego tak jest: x2 >5 <=> f(5) <0 nie powinno byc f(5)>0 czemu znak zwrocony w inną strone?

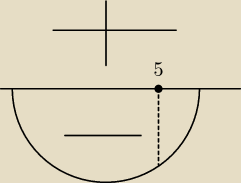
Godzio: f(5) jest poniżej osi X czy powyżej ?

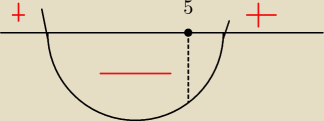
Godzio: tak powinno być poprawnie

Eta: Witam Tak Godzio gdyby f(5) >0 , to wóczas miejsce zerowe byłoby przed 5 dlatego by x₂ >5 to f(5) <0

Eta: Dla Godzia i Pawła zad: Dla jakich wartości parametru "k" równanie: x² +kx +9 =0 ma dwa różne rozwiązania większe od 2.

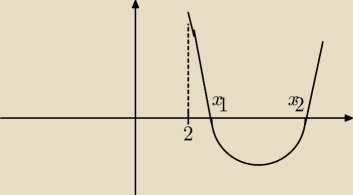
Godzio: x² + kx +9 Δ>0 k² −36>0 k²>36 k>6 v k<−6 x₁ + x₂ >0

−k
	>0
1

k<0 z tego wynika ze k∊(−6,−∞) f(2)>0 4 + 2k +9 > 0 4k>−13

	13		1
k>−		=−6
	2		2

	1
k∊(−6		, −6)
	2

Eta: .........

Godzio: coś umiem

Eta:

Eta: No jeszcze powinieneś zapisać poprawnie przedział: ten : k€( −∞, −6) .....

Godzio: no to tam szczegół

Eta: to ważny "szczegół"

Godzio: będe pamiętać ehh jeszcze jakies 21h i beda prezenty

Eta: Jakich się spodziewasz?

Eta: Dobranoc Wesołych Świąt i udanych

Godzio: Dobranoc , a prezentów to wszystkich nie jestem pewien ale jeden wiem

Paweł: Eta, powiedz mi dlaczego w Twoim przykładzie co podałeś, Godzio zrobil założenie że: x1 + x2 >0 Chyba to nie potrzebne? A tak wogole to Wesołych Swiąt

Godzio: potrzebne zaraz napisze dlaczego

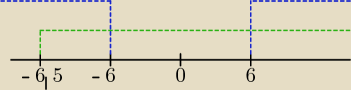
Godzio: 1) k∊(−∞,−6)∪(6,∞)

	1
2) k∊(−6		,∞)
	2

	1		1
( (−∞,−6)∪(6,∞) ) ∩ (−6		,∞) = (−6		,−6)∪(6,∞)
	2		2

ten warunek −> x₁ + x₁ >0 wykluczna nam liczby dodatnie

Paweł: Ale w zadaniu jest ze rozwiazania mają byc wieksze od 2 to czemu ma nam wykluczyć licby dodatnie

Godzio: ale x₁ i x₂ jest rozwiązaniem, a to: x₁+x₂>0 wyklucza nam rozwiązania dodatnie dla k czyli z tego warunku wynika ze k<0 jak wczesniej jest obliczone