Parametr m
Uczen74636: Dla jakich parametrów m równanie x3 − mx + 2 ma trzy rozwiązania . Proszę o wskazówkę od czego
wyjsć . Jest to wielomian wiec pasuje to rozbić albo na czynniki albo podstawić zmienną t.
Ewentualnie graficznie ale nie mam pomysłu od czego wyjsć ...
17 lut 20:54
Janek191:
Szukaj rozwiązań wśród dzielników liczby 2.
17 lut 21:04
Krzysiek: m<0
17 lut 21:05
Krzysiek: Na odwrót, m>0
17 lut 21:06
Krzysiek: m>=4
17 lut 21:09
Janek191:
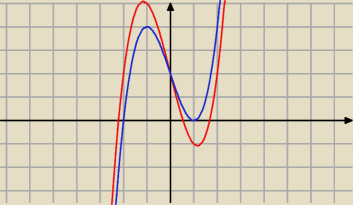
17 lut 21:11
jc: Ja bym próbował tak:
f(x) = x3 − mx + 2
Maksimum lokalne > 0, minimum lokalne < 0.
m> 0, f(√m/3) > 0, f(−√m/3) < 0.
....
17 lut 21:13
Uczen74636: Proszę mi rozpisać te warunki i wyjaśnić dlaczego tak a nie inaczek..
17 lut 21:13
jc: Minimu i maksimum znajdujesz przyrónując pochodną do zera.
Popatrz na wykres. Aby wykres przeciąłą 3 razy oś poziomą, to minimu powinno być poniżej zera,
a maksimum powyżej. Poza tym, jak widzimy minimum wypada po prawej stronie (ojjej, pmyliłem
nierówności!).
m >0, f(p{m/3)) < 0, f(√m/3) > 0.
17 lut 21:18
Uczen74636: Tak ale mógłby mi ktoś pokazać krok po kroku ta pochodna ? Nie za bardzo potrafię takie coe
rozwiazac, a co z zalozeniami?
17 lut 21:24
jc: Która klasa?
17 lut 21:27
Uczen74636: 3 liceum
17 lut 21:29
jc: Odpowiedź m > 3, ale jak to prosto pokazać?
17 lut 21:41
Uczen74636: Najpierw liczę pochodna wychodzi 3x
2 −m i to potem przyrównuje do zera , rysuje parabole i
tabelkę i znajdują maksimum i minimum

17 lut 21:45
jc: Dla m > 3 mamy
f(1) = 3 − m < 0
f(0) = 2 > 0
Na pewno dla dużych x, f(x) > 0
a dla bardzo małych x (bardzo ujemnych) f(x) < 0
Mamy więc pierwiastek pomiędzy 0 a 1, powyżej 1 i poniżej 0 (razem 3).
Dla m=3 mamy dwa pierwastki (jeden podwójny).
A z odpowiedzią dla m < 3 poczekaj chwilę.
17 lut 21:48
jc: Eee, ... wtedy minimum osiągane w √m/3 jest dodatnie i wykres tylko raz przecina oś poziomą.
17 lut 22:00
jc: A dla ujemnych m, funkcja jest rosnąca i na pewno ma tylko jeden pierwiastek.
Nie podoba mi się to rozwiązanie....
17 lut 22:01
Mila:
Nie ma w treści, że współczynniki całkowite?
wtedy, jak podpowiada
Janek
Δ=0⇔
m
3−27=0
m=3
x
3 − 3x + 2=0
W(1)=1−3+2=0
1 0 −3 2 x=1
1 1 −2 0
x
3−3x+2=(x−1)*(x
2+x−2)
Δ=9
x=−2 lub x=1
x
3−3x+2=(x−1)
2*(x+2)
17 lut 22:08
piotr: f'(x)=3x2−m
f''(x)=6x
f'(x)=0 dla
x=−√m/3 maksimum bo f''(−√m/3)<0
i dla
x=√m/3 minimum bo f''(√m/3)>0
warunek aby f'(x) miała dwa miejsca zerowe:
w1. m>0
warunki aby były trzy przecięcia wykresu f(x)
w2. f(−√m/3)>0 ⇔ (−√m/3)3−m(−√m/3)+2>0 m>0
w3. f(√m/3)<0 ⇔ (√m/3)3−m√m/3+2<0 ⇒ m>3
gdy zajdą trzy warunki jednocześnie:
(w1 ∧ w2 ∧ w3) ⇒ m>3
17 lut 22:12
Mila:
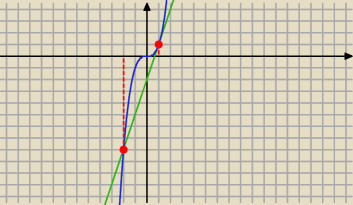
Dla m=3 ma dwa rozwiązania.
f(x)=x
3
g(x)=3x−2
tgα=3
zatem m>3 ale to nie wszystko.
Dalej trzeba pomyśleć nad dalszym ograniczeniem.
17 lut 22:39
piotr: dla m=3 ma dwa rozwiązania: −2 i 1 jako podwójne
natomiast dla m>3 rozwiązań jest trzy
17 lut 23:01
Mila:
Tak.
Tylko zastanawiam się jak wykorzystać ten fakt, że dla m=3 są dwa rozwiązania
do Twojego wniosku nie licząc pochodnych.
17 lut 23:13
Mila:
Trzy różne pierwiastki rzeczywiste:
−m
3+27<0
m
3−27>0
m>3
==========
17 lut 23:21
Bogdan:
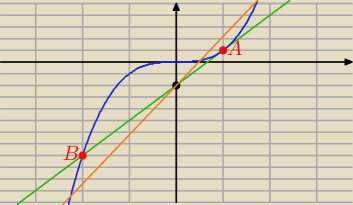
x
3 − mx + 2 = 0
y = x
3 i y = mx − 2
styczna do y = x
3 w punkcie A = (x
0, x
03):
y = y'(x
0)*(x − x
0) + x
03 ⇒ y = y'(x
0)x − y'(x
0)*x
0 + x
02
gdzie: m = y'(x
0) i −2 = −y'(x
0)*x
0 + x
02
y' = 3x
2, y'(x
0) = 3x
02,
−2 = −3x
02*x
0 + x
03 ⇒ x
0 = 1, A = (1, 1), m = y'(1) = 3*1
2 = 3
Liczba m jest współczynnikiem kierunkowym prostej y = mx − 2, dla m = 3 ta prosta
jest styczną do krzywej y = x
3 w punkcie (1, 1) i przecina ją w punkcie B = (−2, −8).
Jeśli m > 3 to prosta y = mx − 2 jest sieczną krzywej y = x
3 i wtedy ma z nią 3 punkty
wspólne.
17 lut 23:37
Mila:
Właśnie myślałam o stycznej,( 22:39) ale to górne ograniczenie mnie niepokoiło.
Ładny rysunek i wytłumaczenie.
Dziękuję
Bogdan 
17 lut 23:42
Bogdan:
Poszedłem
Mila Twoim tropem

17 lut 23:44
Mila:

17 lut 23:45
jc: Jak pokazać elementarnie (bez pochodnych i strasznych rachunków), że w przedziale (0,3) mamy
tylko jeden pierwiastek.
17 lut 23:51
jc: Mam!
suma pierwiastków = 0 (bo nie ma wyrazu z x)
iloczyn pierwiastków = −2, a więc mamy 2 dodatnie pierwiastki i jeden ujemny
Niech to będą liczby a, b, −a−b (a,b >0)
Mamy f(x)=(x−a)(x−b)(x+a+b) = x3 − (a2+b2+ab) x + ab(a+b)
a2 + b2 +ab = m
ab(a+b) =2
√ab < (a+b)/2 (o ile a≠b). Zatem ab < 1 i a+b > 2
Stąd m = (a+b)2 − ab > 4 − 1 = 3
18 lut 00:14


 Dla m=3 ma dwa rozwiązania.
f(x)=x3
g(x)=3x−2
tgα=3
zatem m>3 ale to nie wszystko.
Dalej trzeba pomyśleć nad dalszym ograniczeniem.
Dla m=3 ma dwa rozwiązania.
f(x)=x3
g(x)=3x−2
tgα=3
zatem m>3 ale to nie wszystko.
Dalej trzeba pomyśleć nad dalszym ograniczeniem.
 x3 − mx + 2 = 0
y = x3 i y = mx − 2
styczna do y = x3 w punkcie A = (x0, x03):
y = y'(x0)*(x − x0) + x03 ⇒ y = y'(x0)x − y'(x0)*x0 + x02
gdzie: m = y'(x0) i −2 = −y'(x0)*x0 + x02
y' = 3x2, y'(x0) = 3x02,
−2 = −3x02*x0 + x03 ⇒ x0 = 1, A = (1, 1), m = y'(1) = 3*12 = 3
Liczba m jest współczynnikiem kierunkowym prostej y = mx − 2, dla m = 3 ta prosta
jest styczną do krzywej y = x3 w punkcie (1, 1) i przecina ją w punkcie B = (−2, −8).
Jeśli m > 3 to prosta y = mx − 2 jest sieczną krzywej y = x3 i wtedy ma z nią 3 punkty
wspólne.
x3 − mx + 2 = 0
y = x3 i y = mx − 2
styczna do y = x3 w punkcie A = (x0, x03):
y = y'(x0)*(x − x0) + x03 ⇒ y = y'(x0)x − y'(x0)*x0 + x02
gdzie: m = y'(x0) i −2 = −y'(x0)*x0 + x02
y' = 3x2, y'(x0) = 3x02,
−2 = −3x02*x0 + x03 ⇒ x0 = 1, A = (1, 1), m = y'(1) = 3*12 = 3
Liczba m jest współczynnikiem kierunkowym prostej y = mx − 2, dla m = 3 ta prosta
jest styczną do krzywej y = x3 w punkcie (1, 1) i przecina ją w punkcie B = (−2, −8).
Jeśli m > 3 to prosta y = mx − 2 jest sieczną krzywej y = x3 i wtedy ma z nią 3 punkty
wspólne.


