stereo Metis: Pytanie: Czy istnieje ostrosłup prawidłowy trójkątny, w którym kąt między dwiema sąsiednimi ścianami bocznymi jest rozwarty?

Metis: Nie istnieje prawda? Zastanawiam się nad przypadkiem w jednym z zadań. Co jeśli sciany boczne są trójkatami rozwartokatnymi ?

piotr: oczywiście istnieje wyobraź sobie bardzo "niski" ostrosłup prawidłowy dla zmniejszającej się wysokości przy stałej podstawie kąt, o którym mowa dąży do 180◯

prosta: a kąt płaski ściany bocznej przy wierzchołku ostrosłupa dąży do 120^o ..gdyby krawędzie boczne były rozciągliwe np.gumowe..to wyciągając w górę wierzchołek ostrosłupa zmniejszamy kąt płaski ściany bocznej przy wierzchołku

Bogdan:

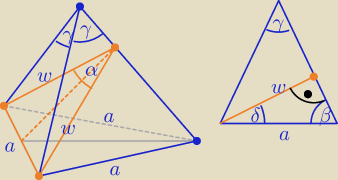
	1
γ∊(0o, 120o), cosγ∊(−		, 1)
	2

	γ		γ		γ
β = 90o −		, δ =		, w = acosδ = acos
	2		2		2

z twierdzenia cosinusów:

	2w2 − a2		γ   2cos2 − 1   2		cosγ
cosα =		=		=
	2w2		γ   2cos2 − 1 + 1   2		cosγ + 1

Jeśli α jest kątem rozwartym, to cosα < 0

cosγ		1
	< 0 ⇒ cosγ ∊ (−		, 0) ⇒ γ ∊ (90o, 120o)
cosγ + 1		2

Ostrosłup, w którym kąt dwuścienny między sąsiednimi ścianami bocznymi jest rozwarty − istnieje, miara kąta płaskiego przy wierzchołku należy do przedziału (90^o, 120^o).

Kacper:

Metis: Dzięki!