Wyznacz tangens kąta DAB
Infinite: Dany jest trójkąt równoboczny ABC. Punkt D leży na boku BC. Wyznacz tangens kąta DAB, jeśli
stosunek pola trójkąta ADB do pola trójkąta ADC wynosi 1:2.
Długo już siedzę nad tym zadaniem i nie wiem jak je zrobić. Wynik mi wyszedł zły. Prawidłowa
odpowiedź to √3/5
Proszę o pomoc ; )
17 lut 20:16
Bogdan:
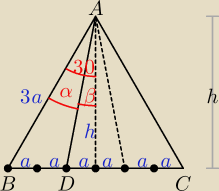
Np. tak:
| | 1 | | 1 | |
PADB = |
| *2a*h = ah, PADC = |
| *4a*h = 2ah |
| | 2 | | 2 | |
| | a | | a | | 1 | |
h = 3a√3, tgβ = |
| = |
| = |
| |
| | h | | 3a√3 | | 3√3 | |
| | tg30o − tgβ | |
tgα = tg(30o − β) = |
| = ... |
| | 1 + tg30o * tgβ | |
17 lut 20:36
Infinite: Dziękuję : )
17 lut 20:43
Bogdan:
Oczywiście długość boku trójkąta jest równa 6a
17 lut 20:43
Infinite: a ten bok AB nie powinien mieć długości 6a bo na rysunku jest 3a?
17 lut 20:44
Infinite: w tym samym momencie zaczęłam pisać : p ok
17 lut 20:46
Eta:
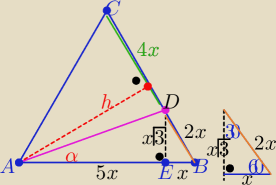
| | |DE| | | x√3 | | √3 | |
tgα= |
| = |
| = |
| |
| | |AE| | | 5x | | 5 | |
17 lut 20:51
Eta:
Podaję dokładniejsze objaśnienia :
| | P(BAD) | | 1 | |
Z treści zadania |
| = |
| |
| | P(DAC) | | 2 | |
te trójkąty mają wspólną wysokość
h opuszczoną da podstawy
zatem |BD|=2x i |DC|=4x , x>0 i |AB|=6x
Korzystamy z trójkąta BED "ekierki" o kątach 30
o,60
o, 90
o
i .................
17 lut 20:56
Bogdan:
17 lut 20:56
Eta:
17 lut 20:57
Infinite: ooo, bardzo dziękuję
17 lut 20:59
Bogdan:
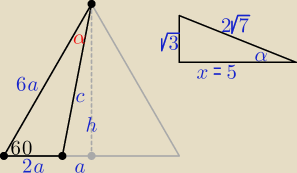
można jeszcze i tak:
c =
√a2 + h2 = 2a
√7
Z tw. sinusów:
| c | | 2a | | | | √3 | |
| = |
| ⇒ sinα = |
| = |
| |
| sin60o | | sinα | | 2a√7 | | 2√7 | |
| | √3 | |
x2 = 28 − 3 = 25, x = 5, tgα = |
| |
| | 5 | |
17 lut 21:12