wielomiany
Haytham: 1. Dla jakich wartości parametru m równanie x4 + 2(m−2)x2 + m2−1 = 0 ma dwa różne
rozwiązania?
No to tak:
podstawiam x2=t, t>=0
i dalej nie wiem czy te warunki, które myślę, są poprawne:
1) Δ>0 2) Δ=0
t1*t2<0 t1+t2>0
I mam pytanie: czy tak? jak nie tak to jak?
17 lut 18:50
wiatr: dwa "różne" rozwiązania czyli
Δ>0
i wzory Vieta tutaj nie są potrzebne, bo nie masz napisane czy mają być różnych znaków czy
jakieś inne.
17 lut 18:54
Jack: 1) ok
2) ok
17 lut 18:55
Haytham: ty
17 lut 19:03
olekturbo: Jack
skad sie wzielo
t1t2 < 0
t1+t2 > 0
17 lut 19:07
Jack: 1) skoro maja byc 2 rozwiazania a my mamy funkcje do czwartej to jeden z pierwiastkow musi byc
ujemny a drugi dodatni bo wtedy
x2 = ten ujemny (czyli tu odpada nam)
i ten drugi dodatni czyli x2 = cos dodatniego, stad mamy 2 rozwiazania
2)
t1 + t2 > 0
dla delty = 0 mamy jeden pierwiastek podwojny , czyli t1 = t2
skoro mamy tylko jeden to musi byc on dodatni zeby x2 = cos dodatniego, zebysmy uzyskali 2
rozwiazania
17 lut 19:14
olekturbo: ah no tak ja glupi
17 lut 19:16
olekturbo: to w takim razie w 2) nie trzeba t1t2 > 0?
17 lut 19:18
Jack: skoro t1 = t2
a t1 + t2 > 0
to t1 * t2 nam nie potrzebne , bo wiadomo ze jest dodatnie...
17 lut 19:20
olekturbo: ok
17 lut 19:21
Haytham: nie wiem jak panowie myślicie, bo z reguły myślę inaczej, ale jak się pozbędę t1*t2>0
to mi nie wyjdzie zgodnie z odpowiedzią, więc to raczej potrzebne
17 lut 19:23
Jack: ale mowimy tylko o drugim przypadku gdzie t1 * t2 jest nie potrzebne bo wystarczy
t1 + t2...
17 lut 19:45
Mila:
1) Δ=0 i t
0>0
lub
2) Δ>0 i t
1*t
2<0
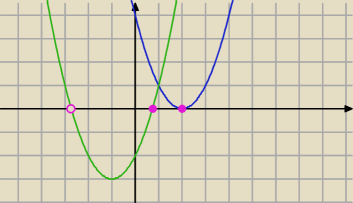
Dwie sytuacje , jak na rysunku.
17 lut 21:47