Ostrosłup
Ania: Krawedz boczna ostrosłupa prawidłowego trojkatnego ma długosc 2
√7 .Sciana boczna tego
ostrosłupa jest nachylona do płaszczyzny podstawy pod katem 60 stopni .Oblicz tangens kata
nachylenia krawedzi bocznej ostrosłupa do płaszczyzny podstawy oraz objetosc tego ostrosłupa.
Mam wyznaczone H (wysokość ostrosłupa) =
√33 h
a z pitagorasa mając ten odcinek od środka jakby trójkąta (podstawy) H
2+(
23)
2 = (2
√7)
2
i wyszło mi ,że h = 6. Natomiast dalej nie mam pomysłu na rozwiązanie. Proszę o pomoc

17 lut 16:37
dero2005:
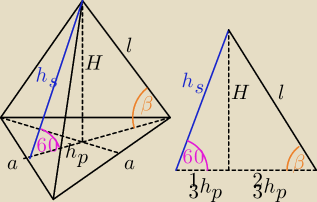
l = 2
√7
l
2 = (
23h
p)
2 + H
2
oblicz H i h
p
potem
17 lut 17:35
Eta:
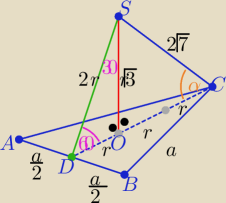
r>0
z twierdzenia Pitagorasa w ΔOCS : 3r
2+4r
2= (2
√7)
2 ⇒ r=2
to z trójkąta DOS "ekierki" o kątach 30
o,60
o,90
o
| | a√3 | |
H= r√3= 2√3 i r= |
| ⇒ .... a= 4√3 i hp=3r= 6 |
| | 6 | |
| | H | |
tgα= |
| = ............... |
| | 2r | |
| | a2√3 | |
V= |
| *H=.............. |
| | 4 | |
dokończ
17 lut 17:42
Eta:

17 lut 17:42
Eta:
Ania .....poszła na randkę

17 lut 17:48
Ania: tgα=
2 √32*2
i tu wychodzi
√32
A V = u{48
√3} / 4 * 2
√3
I to wszystko wyliczyć i elegancko jest ?

17 lut 17:55
dero2005:
niestety , pomylilem się, wzór drugi od góry
17 lut 17:56
Ania: Wyszło V= 24 √3
a α= ? jeśli mi tg wyszedł √32 ?
17 lut 18:00
dero2005:
miałaś policzyć tg a nie wartość kąta
17 lut 18:07
Ania: A tak racja , czyli wszystko jasne

Dzięki ludzie !
17 lut 18:09

 l = 2√7
l2 = (23hp)2 + H2
l = 2√7
l2 = (23hp)2 + H2
 r>0
r>0



 Dzięki ludzie !
Dzięki ludzie !