dowod xxxy: Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C i obwodzie równym 2p . Na prostej AB obrano punkty D i E leżące na zewnątrz odcinka AB takie, że AD=AC i BE=BC.Wykaż, że promień okręgu opisanego na trójkącie ECD jest równy p√2. Doszłam do postaci że kąt ECD= 90 +α/2 +β/2= 90 +1/2 (α+β) Bardzo proszę o wyjaśnienie co dalej.

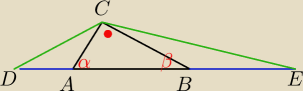
Qulka: jeśli α i β to kąty tego pierwszego to ich suma =90°

Qulka:

	2p		2p
więc R=		=		= √2p
	2sin135°		√2

xxxy: Chwilowe zaćmienie, dzięki