oblicz pole trójkąta jeśli orekle: Oblicz pole trójkąta ABC jeśli A(−5,4)B(−1.1).C(−2,6)

5-latek: Zrob rysunek Pole trojkata np.

	1
1) P=		a*b*sinα
	2

2. Policz dlugosci bokow i wzor Herona sa tez inne sposoby

Janek191: → AB = [ − 1 −(−5 ), 1 − 4] = [ 4, − 3 ] → AC = [−2 − (−5), 6 − 1] = [ 3, 5 ] Pole Δ ABC → → P = 0,5*I det ( AB , AC ) I = 0,5 *I 4*5 − (−3)*3 I = 0, 5 *I 29 I = 14,5

orekle: mi jakimś cudem wyszlo

	19√18
5*
	18

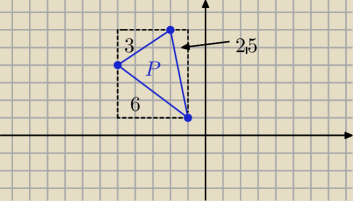
Eta: P(prostokąta)= 4*5=20 P(Δ)= 20−11,5=..........

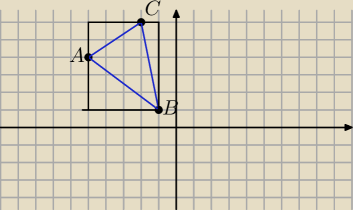
Janek191: Pomyłka → AC = [ −2 − (−5), 6 − 4 ] = [ 3, 2 ] więc P = 0,5* I 4*2 − (− 3)*3 I = 8,5 ======================== II sposób P = 4*5 − 0,5*4*3 − 0,5*5*1 − 0,5*3*2 = 20 − 6 − 2,5 − 3 = 8,5

Eta:

Eta: Janek Ładnie to tak ? kopiować moje rozwiązanie(

Janek191: Widać gołym okiem, ze nie jest skopiowane

The City: mając 3 wierzchołki możesz podstawiać pod wzór z tablic

	1
PΔABC =		|(xB − xA)(yC − yA) − (yB − yA)(xC − xA)|
	2

gdzie A=(x_A, y_A), B=(x_B, y_B), C=(x_C,x_C)

jc: B−A = (−1,1) − (−5,4) = (4,−3) C−A = (−2,6) − (−5,4) = (3, 2) wyznacznik = 8 + 9 = 17 Pole = 17/2

Eta: P=8,5 j²

Kacper: Ja bym policzył jeszcze inaczej 8+1,5−1=8,5 [j²] Zgadnijcie skąd takie coś

jc: Z Ety rysunku mozna odczytac pole: 4*5 − 5/2 − 2*3/2 − 3*4/2 = 20− 2 − 1/2 − 3 − 6 = 8 1/2

jc: A po co [j²]?

jc: @Kacper. Ze wzoru Picka?