zad matthew: zad.1 Punkty A=(−3; 2) B=(4,1) C=(0, −3) są wierzchołkami trójkąta ABC. wyznacz rownanie prostej zawierającej wysokość trójkąta ABC poprowadzoną z wierzchołka A zad2 W trojkącie ABC długość boków AB = 4√5 i BC = 8, a miary kątów przy wierzchołkach A i C są równe odpowiednio 45^o i 60^o. Wysokość poprowadzona z wierzchołka B dzieli trójkąt ABC na dwa trójkąty prostokątne. Oblicz stosunek pól tych trójkątów. Zrobiłem tak: Δ ABD 45^o + 90^o + α₂ = 180^o α₂ = 45^o sin45^o = U{a}{4√6

√2		a
	=
2		4√6

2a = 4√12 a = 2*2√3 a = 4√3

	1
P1 =		* 4√3 * 4√3=
	2

= 2√3 * 4√3 = 8*3 = 24 Δ DBC 60^o + 90^o + α₁=180^o α₁ = 180^o − 150 = 30^o

	b
sin30o =
	8

1		b
	=
2		8

2b = 8 b = 4

	1
P2 =		*4√3 * 4 = 2√3 * 4 = 8√3
	2

stosunek pól trójkątów:

P1		24		8√3		192√3
	=		*		=		= √3
P2		8√3		8√3		192

Nie jestem pewny, czy dobrze zrobiłe.... Może ktoś sprawdzić mi to zadanie dziękuję

Godzio: sprawdzam

kaz: Ad.1) wyznacz równanie pr.BC,a następnie równanie pr.prostopadłej do pr. BC przechodzącej przez punkt A(−3,2)

Godzio: teraz 1 pytanie w treści napisałeś AB = 4√5 a w w obliczeniach 4√6 napisz które jest prawidłowe

matthew: Powinno być 4√6 sorry...

Godzio: wszystko dobrze tylko jak rozszerzasz ułamek nie musisz rozszerzać o liczbe przy pierwiastku

24		3		√3		3√3
	=		*		=		= √3
8√3		√3		√3		3

Godzio: z pierwszym poradzisz sobie ?

matthew: Myslę, że tak, jeszcze podam własne rozwiązanie dzieki za sprawdzenie

matthew: Wyszło mi, że prosta ma wzór y = −x − 1.... dzieki kaz

Godzio: czekaj sprawdze, bo mi wyszło y=7a−3

Godzio: a nie, dobrze ja policzyłem dla wysokość z C

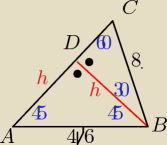
Li : A może prościej ΔABD jest prostokątny i równoramienny więc jego pole = ¹₂Pkwadratu o boku dł = h IABI= d (kwadratu) = h√2 to: h√2= 4√6 => h= 4√3 więc PΔABD= ¹₂*16*3= 24 zatem: PΔBDC= ¹₂*h*IBCI*sin30^o = ¹₂*4√3*8*¹₂= 8√3

	PΔABE		24
więc		=		= √3
	PΔBEC		8√3

Wynik taki sam , ale o ile mniej obliczeń