f wymierna z parametrem
desperatka: Wyznacz wszystkie wartości parametru m dla których zbiorem rozwiązań nierówności ((m−3)
x2+4x+m−3)/(−2x2+x−1)>0 jest zbiór wszystkich liczb rzeczywistych.
16 lut 21:35
===:
rzeczywiście desperatka ... zdesperowana ... ile razy to jeszcze zamieścisz?

16 lut 21:50
desperatka: dopóki nie uzyskam pomocy

16 lut 21:53
===:
| (m−3)x2+4x+m−3 | |
| >0 |
| −2x2+x−1 | |
Analizujemy mianownik ... łatwo zauważysz, że przyjmuje on tylko wartości ujemne
(a<0 Δ<0)
wiesz co z tego wynika

?
16 lut 21:57
===:
Tyle i aż tyle, że aby nierówność była spełniona dla x∊R to licznik też ma przyjmować tylko
| | minus | |
wartości ujemne ( |
| >0 ) |
| | minus | |
założenia dla mianownika to zatem:
m−3<0 ⋀ Δ<0
dalej już sama

16 lut 22:07
wiatr: i sie wszystko wyjasnilo

16 lut 22:08
===:
oczywiście błąd ... nie założenia dla mianownika a
licznika 
16 lut 22:10
===:
1)
m−3<0 ⇒ m<3
2)
Δ=16−4(m−3)2=16−4m2+24m−36=−4m2+24m−20
−4(m2−6m+5)<0
m2−6m+5>0
Δ1=36−20 √Δ=4
m1=5
m2=1
Ostatecznie m<1
16 lut 22:18
===:
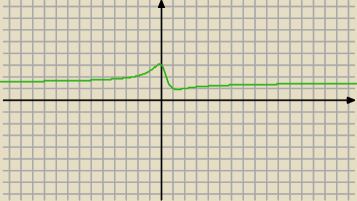
np dla m=0
16 lut 22:21


 ?
?



 np dla m=0
np dla m=0