Liceum Pochodne Paulina: Wyznacz przedziały monotoniczności i ekstrema funkcji f danej wzorem

	4x2+1
f(x)=
	x

Kacper: To licz pochodną.

piotr:

	1		4 x2+1
dla x=−		max {		}=−4
	2		x

	1		4 x2+1
dla x=		min {		}=4
	2		x

piotr:

d		4 x2+1		1
	(		)=4−
dx		x		x2

Paulina: Do tego doszłam. Mam problem z wyznaczeniem monotoniczności, ponieważ nie wiem czy zero "odbija się" czy nie.

Janek191:

	4 x2 + 1		1
f(x) =		= 4 x +		; x ≠ 0
	x		x

więc

	1
f '(x) = 4 −		= 0 ⇔ x = − 0,5 lub x = 0,5
	x2

oraz

	2
f ''(x) =
	x3

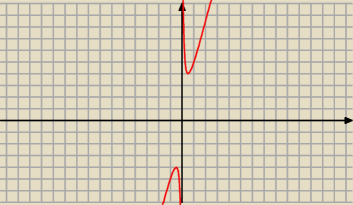
więc f ''( −0,5) < 0 − f . ma maksimum lokalne f ''( 0,5) > 0 − f. ma minimum lokalne oraz funkcja rośnie w ( − ∞ , −0,5) , w ( 0,5, +∞) f maleje w : ( −0,5; 0) , w ( 0 ; 0,5 ) Patrz też na wykres funkcji f.

Janek191: Asymptota pionowa: x = 0

piotr:

	1		1
4−1/x2>0 dla (−∞;−		)∪(		,+∞) ⇒ f(x) rosnąca
	2		2

	1		1
4−1/x2<0 dla (−		;0)∪(0;		) ⇒ f(x) malejąca
	2		2

piotr: asymptota ukośna obustronna w −∞ i w +∞ y=4x

Janek191:

	f(x)
lim		= 4
	x

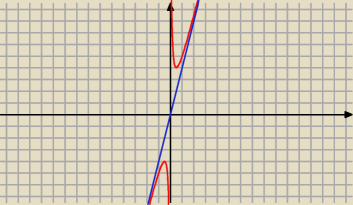
x→∞ Asymptota ukośna: y = 4 x