Twierdzenie Darboux, wielomian, przedział
Darboux: Wykaż, że wielomian w(x)=x3−3x+1 ma w przedziale (0,2) co najmniej jeden pierwiastek.
Dowód z twierdzenia Darboux.
15 lut 15:36
Krzysiek: w(0)=1
w(2)=3
w(1)=−1
Z tego wynika, że w przedziale (0,1) , znajduje się co najmniej jeden pierwiastek. Ale też i
między (1,2) znajduje się co najmniej jeden pierwiastek
15 lut 15:47
Janek191:
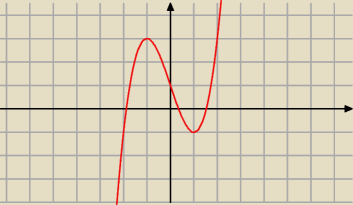
15 lut 16:42
Darboux: Dziękuję. To jest zrozumiałe. Natomiast muszę to jeszcze zapisać za pomocą wzorów.
15 lut 17:24
