asd olekturbo: Wyznacz wszystkie wartości parametru a, dla których nierówność x²+4|x−a| − a² ≥ 0 jest spełniona dla wszystkich liczb rzeczywistych. Zrobiłem to tak: dla x ≥ a x²+4(x−a)−a² ≥ 0 x²+4x − (4a+a²) ≥ 0 zał: Δ ≤ 0 16 + 16a + 4a² ≤ (2+a)² ≤ 0 2+a ≤ 0 a ≤ −2 dla x < a x²−4x−(a²−4a) ≥ 0 Δ ≤ 0 ⇔ 16 + 4a²−16a ≤ 0 (a−2)² ≤ 0 a−2 ≤ 0 a ≤ 2 ale to jest zle bo wynik dobry jest <−2, 2> jak nalezy to poprawnie rozwiazac

Jack: (2+a)² ≤ 0 ≠ (2+a) ≤ 0

Jerzy: Wystarczy , aby: Δ ≤ 0

olekturbo: to jak to zrobic bo nie mam pojecia

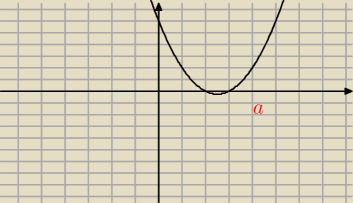
PW: Błąd popełniasz w tym momencie, gdy dla nierówności o ograniczonej dziedzinie (x ≥ a) uznajesz, że warunkiem koniecznym jest Δ ≤ 0. Wyróżnik Δ jest narzędziem opisu zachowania funkcji na całej osi. Nierówność rozpatrywana na kawałku osi może być spełniona w całej dziedzinie, mimo że Δ > 0.

olekturbo: Jakies rady?

PW: Z powodu takiej trudności myślę, że dobrze byłoby spojrzeć tak (x−a)(x+a) + 4|x−a| ≥ 0

	x−a
(1)		(x+a) ≥ − 4.
	|x−a|

Liczba a jest rozwiązaniem nierówności zawsze, natomiast dla pozostałych a dopuszczalne jest dzielenie przez dodatnie |x − a|. Ułamek po lewej stronie (1) jest równy 1 lub −1. W ten sposób mamy do rozwiązania alternatywę dwóch nierówności liniowych. Spróbuj tym tropem.

olekturbo: Oo. dziekuje Sprobuje