Oblicz asymptotę pionową, poziomą i ukośną. bubu: znajdź asymptoty funkcji: x³−2x²+1 f(X)= −−−−−−−−−−−−−−−−−−−−−−−− x²−2x+1 Proszę o pomoc. Pozdrawiam!

Jaś: podziel jedno przez drugie. dalej już mam nadzieję, że będziesz wiedział

bubu: Mogę jeszcze prosić o wzorki na poszczególne asymptoty, bo nie wiem czy mam je dobrze zapisane. Pozdro

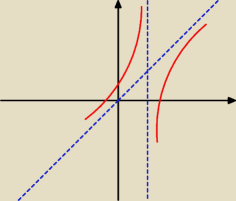
Bogdan: Pomijam zapis →∞ pod lim, rysunek przedstawia szkic wykresu funkcji. D_f: x∊R \ {1} Wyznaczenie asymptoty pionowej: lim_x→1⁻ f(x) = +∞ lim_x→1⁺ = −∞ Istnieje asymptota pionowa x = 1 Wyznaczenie asymptoty poziomej:

	x3 − 2x2 + 1
dla x→−∞: lim		= −∞
	x2 − 2x + 1

	x3 − 2x2 + 1
dla x→+∞: lim		= +∞
	x2 − 2x + 1

Brak asymptoty poziomej. Wyznaczenie asymptoty ukośnej.

	x3 − 2x2 + 1		1		x3 − 2x2 + 1
lim(		*		) = lim		= 1
	x2 − 2x + 1		x		x3 − 2x2 + x

Istnieje asymptota ukośna y = ax + b, a = 1

	x3 − 2x2 + 1
b = lim(		− x ) =
	x2 − 2x + 1

	x3 − 2x2 + 1 − x3 + 2x2 − x		1 − x
= lim		= lim		= 0
	x2 − 2x + 1		x2 − 2x + 1

Asymptota ukośna y = x

Ania: ale jak sie oblicza te asymptoty krok po kroku.... jakie są podstawowe zasady...

KM: http://pl.wikipedia.org/wiki/Asymptota

miet: ∫vdx

paulaa: c) (√3) do potegi 4 (√3) do potegi −2 (√3) do potegi − 6 d) (√2) do potegi 6 (√2) do potegi 7 (√2) do potegi −8 obliczyc

jiji: 5²+2³

mk: (x2+x+1)/(x+1)

boogie: 1/√x−2

lenonek: jak zaznaczyć oraz jak obliczyć asymptotę poziomą? bo ja dalej nie rozumiem

huehuehue: wzor na asympote pozioma y=ax+b gdzie:

	f(x)
a=limx→∞
	x

b=limx→∞ f(x) − ax

12345: zadanie Narysuj wykres funkcji y = 2^x+2 + 3, a następnie omów jej własności (równanie asymptoty poziomej, zbiór wartości, monotoniczność). Jak wykonać takie zadanie?

asdf: liczysz dziedzine i na krancach dziedziny liczysz granice obustronne, np (jakas inna funkcja − zeby nie namieszac): f(x): D: x e (−∞;−1)(−1;∞) i jezeli: lim_x−>−1⁻ f(x) = ± ∞ lim_x−>−1⁺ f(x) = ± ∞ to w punkcie x = −1 istnieje asymptota pionowa. http://www.etrapez.pl/blog/pochodne/asymptoty-2/asymptoty-poziome-i-ukosne-funkcji/

12345: nie potrafię sobie tego wyobrazić co to jest "lim_x"?

asdf: a miałeś/aś granice?

12345: tzn? nie wiem, poddaje się, nie mam pojęcia o co chodzi ale jak możesz − spróbuj wytłumaczyć trochę prościej, tak na poziomie podstawowym.

asdf: nie wiesz czy miales/as takie cos jak granice ciągu / funkcji? odpowiedź jest banalnie prosta: tak / nie? Na poziomie podstawowym to jakim?

12345: nie

12345: dzięki za pomoc już wiem o co chodzi

12345: potrzeba było wielokrotnego czytania i przetłumaczenia sobie na swój język

12345: ccc