Przygotowanie do matury #24 The City: Polecenie: Zaznacz w układzie współrzędnych zbiór rozwiązań układu nierówności.

	⎧	|x+y|≤4
e)	⎩	|x−y|≤4

	⎧	|y|≤|x|
f)	⎩	|x|≤3

Wczoraj Mila wytłumaczyła mi jak rozwiązywać układy podobne do tego

⎧	y<2−|x−2|
⎩	y>|x|−2

poprzez wyznaczanie przedziałów itd... ale w e) i f) nie wiem jak miałbym wyznaczyć przedziały...

Benny: f) |y|≤|x| y≤|x| ⋀ y≥−|x|

The City: niestety, nie wiem jak to dalej zrobić, bo jak rozbiję to na dwa układy, tj.

⎧	y≤|x|
⎩	|x|≤3

⋁

⎧	y≥−|x|
⎩	|x|≤3

to wówczas chyba nie będzie miało to znaczenia czy było y≤|x| ⋀ y≥ −|x| czy y≤|x| ⋁ y≥ −|x|, a to raczej ważne..

Jerzy: Dla x ≥ 0 i y ≥ 0 masz: y ≤ x Dla x ≥ 0 i y < 0 masz: − y ≤ x Dla x < 0 i y ≥ 0 masz: y ≤ − x Dla x < 0 i y < 0 masz: − y ≤ − x

Godzio: Podpunkt e) |x + y| ≤ 4 ⇒ − 4 ≤ x + y ≤ 4 ⇒ − x − 4 ≤ y ≤ − x + 4 Rysujesz prostą y = −x − 4 oraz prostą y = − x + 4. Obszar, który Cie interesuje znajduje się między tymi prostymi (włącznie z nimi) Podobnie druga część układu. Ostatecznie bierzesz część wspólną (pewnie wychodzi jakiś równoległobok )

The City: Dzięki wszystkim. Za chwilę to przelicze i w razie problemów napisze.

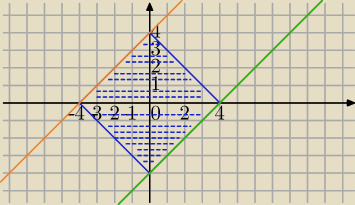
Mila: 1) |x+y|≤4 (niebieski kwadrat , warto zapamiętać) |x−y|≤4 ⇔−4≤x−y≤4 /−x −x−4≤−y≤4−x /*(−1) x−4≤y≤x+4 obszar między prostymi y=x−4 i y=x+4 wynik niebieski kwadrat z brzegiem.