| 1 | ||
to sin2x=0 lub 2sin2x−1=0 to sin2x= | ||
| 2 |
cd.
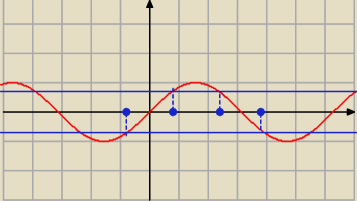
sin2 x = 0 ⇔ sin x = 0 ⇔ x = π*k
| 1 | √2 | √2 | ||||
sin2 x = | ⇔ sin x = − | lub x = | ⇔ | |||
| 2 | 2 | 2 |
| π | 5 | π | 3 | |||||
⇔ x =− | + 2π*k lub x = | π + 2π*k lub x = | +2π*k lub x = | π +2π*k | ||||
| 4 | 4 | 4 | 4 |
| 1 | ||
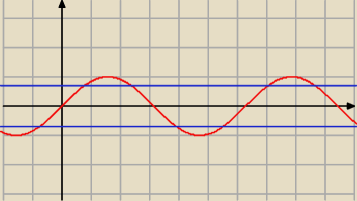
b) sin2 2x = | ||
| 2 |
| √2 | √2 | |||
sin 2x = − | lub sin 2x = | |||
| 2 | 2 |
| π | π | π | π | |||||
2x = π+ | + 2π*k lub 2x =2π− | +2π*k lub 2x= | +2π*k lub 2x = π− | +2π*k | ||||
| 4 | 4 | 4 | 4 |
| 5^2 | 52 |
| 2^{10} | 210 |
| a_2 | a2 |
| a_{25} | a25 |
| p{2} | √2 |
| p{81} | √81 |
| Kliknij po więcej przykładów | |
|---|---|
| Twój nick | |