| x3 | ||
f(x) = | ||
| x2 − 9 |
| 3 x2*(x2 −9) − x3*( 2 x) | 3 x4 − 27x2 − 2 x4 | |||
f '(x) = | = | = | ||
| (x2 −9)2 | (x2 −9)2 |
| x4 − 27 x2 | ||
= | ||
| (x2 − 9)2 |
| x4 − 27 x2 | ||
f '(x) = | ||
| x4 − 18 x2 + 81 |
| (4 x3 − 54 x)*(x4 − 18 x2 + 81) − (x4−27x2)*(4 x3 − 36 x) | ||
f ''(x) = | = | |
| ( x2 −9)4 |
| 6x5 − 1050 | |
| (x2 − 9)4 |
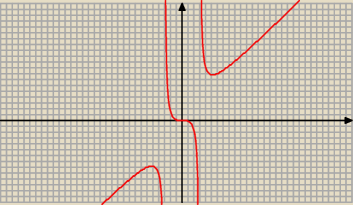 f '(x) = 0 ⇔ x4 − 27 x2 = 0 ⇔ x2*( x2 − 27) = 0 ⇔ x = 0 lub x = −√27 lub x = √27 ⇔
⇔ x = 0 lub x = − 3√3 lub x = 3√3
Policz jeszcze raz II pochodną.
f '(x) = 0 ⇔ x4 − 27 x2 = 0 ⇔ x2*( x2 − 27) = 0 ⇔ x = 0 lub x = −√27 lub x = √27 ⇔
⇔ x = 0 lub x = − 3√3 lub x = 3√3
Policz jeszcze raz II pochodną.
 Dzięki wielkie
Dzięki wielkie