minimum czy maksimum pokolax: funkcja f(x) = ^ax+b_{(x−1)(x−4)} w punkcie x₀=2 ma ekstremum równe −1. ustal, czy jest to minimum czy maksimum

Jerzy: Policz pochodną i pokaż jak zmienia znak

pokolax: ale jak mam ją obliczyć mając w liczniku ax+b?

grzest: Obliczasz pochodną po x, a i b to stałe. Ponadto z treści zadania wynika, że f(2)=−1, f'(2)=0. Stąd można wyliczyć stałe a i b.

Janek191:

	a x + b
f(x) =		; x ≠ 1 i x ≠ 4
	( x −1)*( x − 4)

	a*(x − 1)*(x − 4) − (a x + b)*(2 x − 5)
f '(x) =
	(( x −1)*(x −4))2

f ma w x₀ = 2 ekstremum, więc

	−2 a −( 2 a + b)*(− 1)
f '(2) = 0 , czyli		= 0 ⇔ − 2a +2 a + b = 0 ⇒ b = 0
	4

	2a + b		2a + 0
f(2) = − 1 więc		= − 1 ⇔		= − 1 ⇔ a = 1
	−2		− 2

zatem

	2 x
f(x) =
	(x −1)*(x − 4)

	(x −1)*(x −4) − x*(2 x − 5)
f '(x) =		=
	(( x−1)*(x − 4))2

	x2 − 5 x + 4 − 2 x2 + 5x		− x2 + 4
=		=
	((x−1)*(x−4))2		(x −1)*(x−4))2

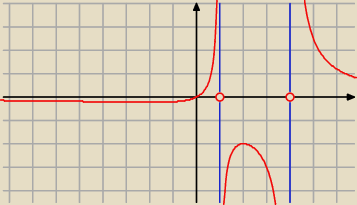
Dla x niewiele mniejszego od 2 jest f '(x) > 0, a dla x niewiele większego od 2 jest f '(x) < 0, czyli funkcja f osiąga w punkcie x₀ = 2 maksimum lokalne.

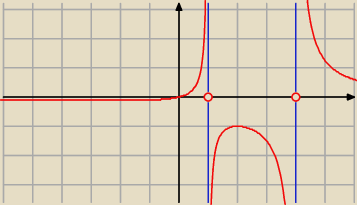
Janek191: Poprawka Tam jest pomyłka − powinno być

	x
f(x) =		, bo a = 1 ( pomyłkowo zapisałem a = 2)
	(x −1)*(x −4)

Wykres będzie następujący:

pokolax: można prosić o wytłumaczenie krok po kroku?

Janek191: Wszystko jest napisane − krok po kroku