Przygotowanie do matury #23
The City:
Zaznacz w układzie współrzędnych zbiór rozwiązań układu nierówności.
przekształciłem do postaci
i pojawił się mój odwieczny problem − ⋁ czy ⋀
"pomiędzy" nierówności wstawiłem ⋀, ale zacząłem się zastanawiać nad wartością bezwzględną.
I tutaj pytanie − jaki jest najlepszy sposób na określenie spójnika w takich przypadkach?
Z góry dzięki
13 lut 22:07
PW: Układ równań (nierówności) to zawsze równania (nierówności) ze spójnikiem "i".
13 lut 22:17
The City:
cokolwiek by się tam nie znalazło? wartości bezwzględne czy inne twory − wszystko "i"?
13 lut 22:20
13 lut 22:33
Mila:
Nie możesz dostać tego samego , bo nie napisałeś dobrze warunków:
y≥x−1
x≥0
lub
y≥−x−1
x<0
Zaraz podam rozwiązanie.
13 lut 22:51
Mila:
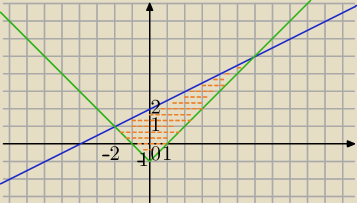
| | 1 | | 1 | |
y≤ |
| x+2 − obszar pod prostą y= |
| x+2 |
| | 2 | | 2 | |
i
y≥|x|−1− obszar nad wykresem funkcji y=|x|−1
13 lut 22:55
The City:
Czyli, że jeżeli z wartości bezwzględnej wyjdą mi 2 przedziały to z jednego układu nierówności
robię dwa w których mam różne dziedziny oraz różne nierówności zamiast tej, która posiadała
wartość bezwzględną; i te dwa układy są połączone spójnikiem "lub", a wszystko co wewnątrz
pojedynczych układów, jest połączone spójnikiem "i"?
13 lut 23:01
Mila:
Tak.
13 lut 23:27
The City:
Super, dziękuje za pomoc

13 lut 23:31

