PW: Dziękuję za ilustrację i tradycyjnie służę wytłumaczeniem

Występująca po lewej stronie równania funkcja jest parzysta. Oznacza to, że jeżeli równanie ma
rozwiązanie dodatnie x
0, to również (− x
0) jest rozwiązaniem. Wystarczy więc ograniczyć się
do rozpatrywania równania dla x > 0.
a) Dla x∊(0, 2) jest x
2 − 4 < 0 i x
2 − 5 < 0, wobec czego równanie przyjmuje postać
− x
2 + 4 − x
2 + 5 = 1, x ∊ (0,2)
− 2x
2 = − 8, x ∊ (0,2)
x
2 = 4, x ∊ (0,2)
− równanie to nie ma rozwiązań.
b) Dla x∊<2,
√5> jest x
2 − 4 ≥ 0 i x
2 − 5 ≤ 0, zatem równanie przyjmuje postać
x
2 − 4 − x
2 + 5 = 1, x∊<2,
√5>
1 = 1, x∊<2,
√5>
− rozwiązaniami są wszystkie liczby z dziedziny.
c) Dla x∊(
√5,
∞) badane równanie ma postać
x
2 − 4 + x
2 − 5 = 1, x∊(
√5,
∞)
2x
2 = 9, x∊(
√5,
∞)
x
2 = 4,5
− równanie to nie ma rozwiązań.
Rozwiązanie b) i wspomniana na początku parzystość dają odpowiedź podaną przez
Qulkę.
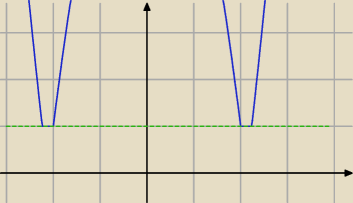 xe<−√5;−2> u <2;√5>
xe<−√5;−2> u <2;√5>
 Występująca po lewej stronie równania funkcja jest parzysta. Oznacza to, że jeżeli równanie ma
rozwiązanie dodatnie x0, to również (− x0) jest rozwiązaniem. Wystarczy więc ograniczyć się
do rozpatrywania równania dla x > 0.
a) Dla x∊(0, 2) jest x2 − 4 < 0 i x2 − 5 < 0, wobec czego równanie przyjmuje postać
− x2 + 4 − x2 + 5 = 1, x ∊ (0,2)
− 2x2 = − 8, x ∊ (0,2)
x2 = 4, x ∊ (0,2)
− równanie to nie ma rozwiązań.
b) Dla x∊<2, √5> jest x2 − 4 ≥ 0 i x2 − 5 ≤ 0, zatem równanie przyjmuje postać
x2 − 4 − x2 + 5 = 1, x∊<2, √5>
1 = 1, x∊<2, √5>
− rozwiązaniami są wszystkie liczby z dziedziny.
c) Dla x∊(√5,∞) badane równanie ma postać
x2 − 4 + x2 − 5 = 1, x∊(√5,∞)
2x2 = 9, x∊(√5,∞)
x2 = 4,5
− równanie to nie ma rozwiązań.
Rozwiązanie b) i wspomniana na początku parzystość dają odpowiedź podaną przez Qulkę.
Występująca po lewej stronie równania funkcja jest parzysta. Oznacza to, że jeżeli równanie ma
rozwiązanie dodatnie x0, to również (− x0) jest rozwiązaniem. Wystarczy więc ograniczyć się
do rozpatrywania równania dla x > 0.
a) Dla x∊(0, 2) jest x2 − 4 < 0 i x2 − 5 < 0, wobec czego równanie przyjmuje postać
− x2 + 4 − x2 + 5 = 1, x ∊ (0,2)
− 2x2 = − 8, x ∊ (0,2)
x2 = 4, x ∊ (0,2)
− równanie to nie ma rozwiązań.
b) Dla x∊<2, √5> jest x2 − 4 ≥ 0 i x2 − 5 ≤ 0, zatem równanie przyjmuje postać
x2 − 4 − x2 + 5 = 1, x∊<2, √5>
1 = 1, x∊<2, √5>
− rozwiązaniami są wszystkie liczby z dziedziny.
c) Dla x∊(√5,∞) badane równanie ma postać
x2 − 4 + x2 − 5 = 1, x∊(√5,∞)
2x2 = 9, x∊(√5,∞)
x2 = 4,5
− równanie to nie ma rozwiązań.
Rozwiązanie b) i wspomniana na początku parzystość dają odpowiedź podaną przez Qulkę.
