sd olekturbo: przez początek układu współrzednych poprowadzono styczne do paraboli o równaniu y =

	1
		x2+3. Oblicz miarę kąta ostrego między stycznymi.
	4

olekturbo: 2) Narysuj w ukladzie wspolrzednych figure bedaca zbiorem punktow, ktorych wspolrzedne (x,y) spelniaja nierownosc x²+y²−6|y| ≤ 9. Oblicz pole tej figury. Nie umiem obliczyc pola.

olekturbo: 3) W ostroslupie prawidlowym czworokatnym krawedz podstawy ma dlugosc a. Kat miedzy krawedzia boczna i podstawa jest rowny katowi plaskiemu przy wierzcholku ostroslupa. Oblicz objetosc ostroslupa. Co to jest kat plaski przy wierzcholku?

Jack: 1) https://matematykaszkolna.pl/strona/1228.html

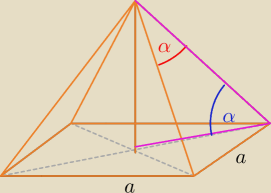
Jack: 3) α − kąt płaski przy wierzchołku α − kąt między krawędzią boczną i podstawą ostrosłupa ja to tak widzę...

Mila: Dobrze widzisz Jack.

olekturbo: A ktos pomoze mi z 3−cim zadaniem? i z obliczeniem pola w 2−gim?

olekturbo: 4) wykaż, że dla dowolnych liczb rzeczywistych a i b prawdziwa jest nierówność: a²+b²+1 > a + b

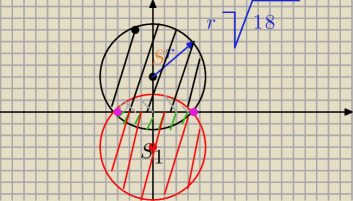
5-latek: W drugim ja bym to widział tak x²+y²−6|y|≤9 1^o)dla y≥0 mamy x²+y²−6y≤9 to (x−0)²+(y−3)²≤9+9 (x−0)²+(y−3)² ≤18 (będzie to czarne kolo srodku S=(0,3) i r=√18 ale bez tego wycinka kolowego zaznaczonego na zielono dla y<0 będzie x²+y²+6y≤9 (x−0)²+(y+3)²≤18 (będzie to czerwone kolo o srodku S₁=(0,−3) i promieniu r=√18 ale bez tego wycinka kolowego zaznaczonego na szaro Obliczysz pole figury czarnej *2 masz pole całej figury Pole wycinka kolowego wiesz jak policzyć Masz rysunek wiec widzisz co i jak

5-latek: Ma być odcinka kola a nie wycinka kolowego .

Kacper:

	1		1		1
(a−		)2+(b−		)2+		>0
	2		2		2

a²−a+b²−b+1>0 a²+b²+1>a+b c.k.d

olekturbo: @5−latek Odpowiedz jest taka

	1		1
P = 2*18pi − 2(		*18pi −		*6*3) = 27pi + 18
	4		2

sam obliczylem pola dwóch kół, czyłi 2*18pi. Oni odejmują od tego wycinek koła i trójkąt. Dlaczego odejmują tez trojkat?

5-latek: https://matematykaszkolna.pl/strona/474.html Zobacz tutaj

KOT: Mam takie pytanko do pierwszego te styczne wyznaczyć pochodną tak ?

KOT: do zadania 1

Qulka: albo że prosta y=ax z tą parabolą ma 1 punkt wspólny czyli Δ=0

yht: Δ=0 chyba jest prościej, bo z pochodną troche kombinacji jest

olekturbo: 1) zrobiłem

1
	x2+3 = mx
4

1
	x2−mx+3 = 0
4

Δ = m²−3 Δ = 0 ⇔ m = −√3 v m = √3 y = √3x v y = −√3x kąt wyszedł 60*

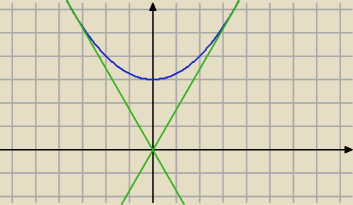
Qulka: zgadza się

olekturbo: Qulka a jak to zrobić za pomocą pochodnej? bo potrafię zrobić jak mam x₀ czy y₀ ale tak z niewiadomą to nie wyszło mi

Qulka: a=x₀/2 podstawiasz (x₀/2)•x₀ =x₀²/4+3 i rozwiązujesz i masz x₀

yht:

	1
masz rownanie stycznej: y=mx i masz f(x)=		x2+3
	4

styczna w punkcie x₀ więc m = f'(x₀)

	1
f'(x) =		x
	2

	1
f'(x0) =		x0
	2

	1
zatem m =		x0
	2

	1
punkt (x0,		x02+3) należy zarówno do f(x), jak i (co ważniejsze) do stycznej
	4

	1
y=		x0 * x
	2

	1		1
wykorzystujemy to że punkt (x0,		x02+3) należy do stycznej y=		x0 * x
	4		2

1		1
	x02+3=		x0 * x0
4		2

1		1
	x02+3=		x02
4		2

x₀² = t

1		1
	t+3=		t
4		2

wychodzi że x₀=√12 lub x₀=−√12

	1
obliczamy		x02+3
	4

1
	*12 + 3 = 6
4

zatem punkty wspólne stycznej i paraboli to (−√12,6) oraz (√12,6) i dalej już prosto

yht: ogólnie pochodnej używaj jeśli masz styczne do wielomianów wyższych (>2) stopni, albo do funkcji wymiernych a jeśli masz stycze do paraboli albo okręgów to używaj tego Δ=0, jest prościej

olekturbo: dzieki. a co jesli nie przechodzi przez punkt 0,0

Qulka: to przechodzi przez jakiś punkt więc uzależniasz b od a i tak samo

olekturbo: ok dzieki bardzo zycze dobrej nocy

yht: to wtedy y=mx+n, podstawiasz za x,y współrzędne punktu przez który przechodzi − masz jakąś zależność między m i n −−> uzależniasz n od m potem liczysz normalnie m = f'(x₀) potem wykorzystujesz że punkt należy do stycznej − wstawiasz jego współrzędne za x,y w stycznej potem za m w stycznej wstawiasz f'(x₀) i masz równanie z (jedną) niewiadomą x₀

KOT: hmm dlaczego to działa to z Δ=0 , ja liczę wtedy punkt styczny do prostej (funkcji liniowej ) czyli prosta jest jakby osią X ?

yht: nie liczysz nigdy stycznej do prostej, tylko do paraboli (ew. wielomianu wyższego stopnia, wymiernej, okręgu itp).

olekturbo: Styczna ma z parabolą jeden punkt wspólny, dlatego delta = 0.