Geometria przestrzenna
Niki: Hej ! Bardzo proszę Was o pomoc w rozwiązaniu zadania z geometrii przestrzennej. Oto ono: Dane
są dwa przystające romby ABCD i DCEF o wspólnym boku DC długości 4 cm. Miara kątów ostrych
tych rombów jest równa: |∡ADC| = |∡DCE|=45stopni . Płaszczyzny zawierające te romby tworzą kąt
dwuścienny o mierze 120 stopni. Oblicz odległość między prostymi AB i EF.
13 lut 16:15
Mila:
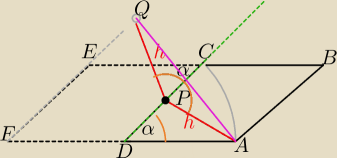
Trudno jest narysować, aby to było widać.
Narysuj na kartce te dwa romby i zegnij kartkę wzdłuż CD.
Punkt Q będzie leżał na przedłużeniu FE (w przestrzeni).
QP⊥AP
∡APQ=120
o − kąt między płaszczyznami.
ΔDPA− Δprostokątny równoramienny
|DP|=|AP|
|AD|
2=h
2+h
2
16=2h
2
h=
√8
W ΔAPQ:
|AQ|
2=
√82+
√82−2*
√8*
√8*cos120
o
|AQ|
2=16+8=24
|AQ|=
√24=2
√6
13 lut 21:33
Niki: Dziękuję bardzo

14 lut 13:04
5-latek: I to się chwali

14 lut 13:05
 Trudno jest narysować, aby to było widać.
Narysuj na kartce te dwa romby i zegnij kartkę wzdłuż CD.
Punkt Q będzie leżał na przedłużeniu FE (w przestrzeni).
QP⊥AP
∡APQ=120o − kąt między płaszczyznami.
ΔDPA− Δprostokątny równoramienny
|DP|=|AP|
|AD|2=h2+h2
16=2h2
h=√8
W ΔAPQ:
|AQ|2=√82+√82−2*√8*√8*cos120o
Trudno jest narysować, aby to było widać.
Narysuj na kartce te dwa romby i zegnij kartkę wzdłuż CD.
Punkt Q będzie leżał na przedłużeniu FE (w przestrzeni).
QP⊥AP
∡APQ=120o − kąt między płaszczyznami.
ΔDPA− Δprostokątny równoramienny
|DP|=|AP|
|AD|2=h2+h2
16=2h2
h=√8
W ΔAPQ:
|AQ|2=√82+√82−2*√8*√8*cos120o

