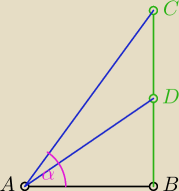
Na płaszczyźnie π dany jest odcinek AB.Odcinek BC jest prostopadły do płaszczyzny π. Punkt D
jest środkiem odcinka BC. Oblicz sinus kąta nachylenia prostej AC do płaszczyzny π, wiedząc,
| 2 | ||
że tanges nachylenia prostej AD do płaszczyzny π wynosi | ||
| 3 |
| |BD| | 2 | ||
= | |||
| |AB| | 3 |
| 2|BD| | 4 | |||
tgα= | = | |||
| |AB| | 3 |
| 4 | ||
sinα= | ||
| 5 |