moduł
Dawid: Witam wie ktoś może jak rozwiazywać równania z wartoscią bezwzględną

?
chodzi mi o równania kwadratowe z wartoscia bezwzględną
co trzeba robić wyznaczyś najpierw miejsca zerowe

?
|x
2 + 4x −5| + |x
2 + 4x|=5
20 gru 23:21
Godzio:
tak

poradzisz sobie ?
20 gru 23:51
Godzio:
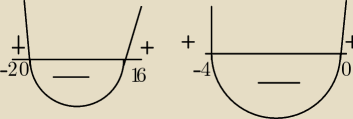
x
2+4x−5 =0
Δ=16 +20=36
√Δ=36
x
2+4x =0
x(x+4)=0
x=0 v x=−4
1
o 2
o 3
o 4
o
−−−−−−−−− −20 −−−−−−−−−−− −4 −−−−− 0 −−−−−−−−−−−− 16
1
o
x∊(−∞,−20>
x
2+4x−5 + x
2 +4x = 5
2x
2 +8x −10 =0 /:2
x
2 + 4x −5 =0
x
2 −x +5x−5=0
(x−1)(x+5) =0
x=1 v x=−5 => rozwiązania nie należą do przedziału x∊∅
2
o
x∊(−20,−4>
−x
2 − 4x +5 +x
2 +4x =5
5=5 => cały przedział spełnia => x∊(−20,−4>
3
o (−4,0)
−x
2−4x+5 −x
2 −4x =5
−2x
2 −8x =0
−x
2−4x =0
−x(x+4) =0
x=0 v x=−4 => nie należą do przedziału => x∊∅
4
o
x∊<0,16)
−x
2−4x+5 +x
2 +4x =5
5=5 => cały przedział => x∊<0,16)
5
o
x∊<16,∞)
x
2+4x−5 +x
2 +4x =5
2x
2 +8x −10=0
x
2 −x +5x−5=0
(x−1)(x+5) =0
x=1 v x=−5 => rozwiązania nie należą do przedziału x∊∅
czyli: x∊(−20,−4>∪<0,16)
wydaje mi się że tak powinno byc dobrze
21 gru 00:05
Li :
[P[Godzio}

x
2 +4x −5= ( x +5)(x −1)
to;
x
1=
−5 v x
2=
1
bo: Δ= 36 to
√Δ=
6 
21 gru 01:30
Godzio:
ehh mały błąd a wszystko źle
21 gru 02:01
Godzio:
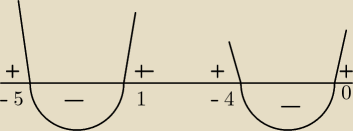
x
2+4x−5 =0
Δ=16 +20=36
√Δ=6
x
2+4x =0
x(x+4)=0
x=0 v x=−4
1
o 2
o 3
o 4
o 5
o
−−−−−−−−− −5 −−−−−−−−−−− −4 −−−−− 0 −−−−−−−−−−1−−−−−−−−−−−
1o
x∊(−∞,−5>
x
2+4x−5 + x
2 +4x = 5
2x
2 +8x −10 =0 /:2
x
2 + 4x −5 =0
x
2 −x +5x−5=0
(x−1)(x+5) =0
x=1 v x=−5 => x=−5
2
o
x∊(−5,−4)
−x
2 − 4x +5 +x
2 +4x =5
5=5 => cały przedział spełnia => x∊(−5,−4)
3
o (−4,0)
−x
2−4x+5 −x
2 −4x =5
−2x
2 −8x =0
−x
2−4x =0
−x(x+4) =0
x=0 v x=−4 => nie należą do przedziału => x∊∅
4
o
x∊<0,1)
−x
2−4x+5 +x
2 +4x =5
5=5 => cały przedział => x∊<0,1)
5o
x∊<1,∞)
x
2+4x−5 +x
2 +4x =5
2x
2 +8x −10=0
x
2 −x +5x−5=0
(x−1)(x+5) =0
x=1 v x=−5 => x=1
czyli: x∊(−5,−4)∪<0,1)∪{−5,1}
to teraz jest już git majonez

21 gru 02:15
 ?
chodzi mi o równania kwadratowe z wartoscia bezwzględną
co trzeba robić wyznaczyś najpierw miejsca zerowe
?
chodzi mi o równania kwadratowe z wartoscia bezwzględną
co trzeba robić wyznaczyś najpierw miejsca zerowe ?
|x2 + 4x −5| + |x2 + 4x|=5
?
|x2 + 4x −5| + |x2 + 4x|=5
 poradzisz sobie ?
poradzisz sobie ?
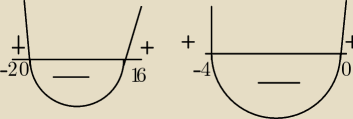 x2+4x−5 =0
Δ=16 +20=36
√Δ=36
x2+4x−5 =0
Δ=16 +20=36
√Δ=36
 x2 +4x −5= ( x +5)(x −1)
to;
x1= −5 v x2= 1
bo: Δ= 36 to √Δ= 6
x2 +4x −5= ( x +5)(x −1)
to;
x1= −5 v x2= 1
bo: Δ= 36 to √Δ= 6 
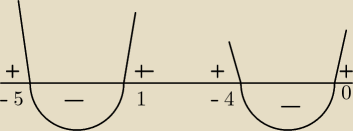 x2+4x−5 =0
Δ=16 +20=36
√Δ=6
x2+4x−5 =0
Δ=16 +20=36
√Δ=6
